Giải bài 6 trang 62 vở thực hành Toán 7
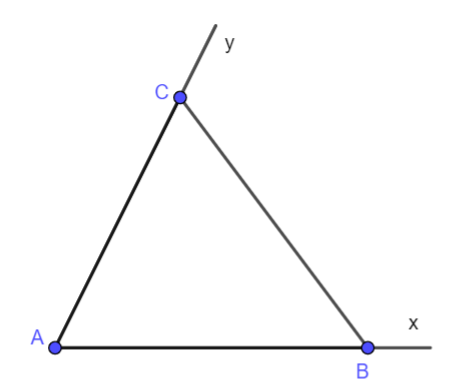
Bài 6. Cho tam giác ABC và cho Bx, Cy lần lượt là các tia đối của các tia BA, CA. Biết \(\widehat {xBC} = \widehat {yCB} = 2\widehat {BAC}\). Hãy tính số đo góc BAC.
Đề bài
Bài 6. Cho tam giác ABC và cho Bx, Cy lần lượt là các tia đối của các tia BA, CA. Biết \(\widehat {xBC} = \widehat {yCB} = 2\widehat {BAC}\). Hãy tính số đo góc BAC.
Phương pháp giải - Xem chi tiết
Tổng hai góc kề bù và tổng ba góc trong một tam giác bằng \({180^o}\).
Lời giải chi tiết
|
GT |
\(\Delta ABC\); Bx, Cy là các tia đối của các tia BA,CA; \(\widehat {xBC} = \widehat {yCB} = 2\widehat {BAC}\) |
|
KL |
Tính \(\widehat {BAC}.\) |
Vì hai góc kề bù có tổng bằng \({180^o}\)nên ta có:
\(\begin{array}{l}\widehat {ABC} + \widehat {xBC} = {180^o} \Rightarrow \widehat {ABC} = {180^o} - \widehat {xBC}\left( 1 \right)\\\widehat {ACB} + \widehat {yCB} = {180^o} \Rightarrow \widehat {ABC} = {180^o} - \widehat {yCB}\left( 2 \right)\end{array}\)
Do tổng ba góc trong tam giác ABC bằng \({180^o}\)nên ta có:
\(\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\left( 3 \right)\)
Từ (1) , (2) và (3) ta suy ra
\(\begin{array}{l}\widehat {BAC} = {180^o} - \widehat {ABC} - \widehat {ACB}\\ \Leftrightarrow \widehat {BAC} = {180^o} - \left( {{{180}^o} - \widehat {xBC}} \right) - \left( {{{180}^o} - \widehat {yCB}} \right)\\ \Leftrightarrow \widehat {BAC} = 2\widehat {BAC} + 2\widehat {BAC} - {180^o} = 4\widehat {BAC} - {180^o}\end{array}\)
Do đó \(3\widehat {BAC} = {180^o} \Rightarrow \widehat {BAC} = {60^o}\).