Giải Bài 62 trang 87 sách bài tập toán 7 - Cánh diều
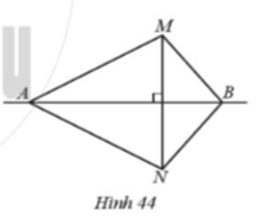
Quan sát Hình 44, biết ∆MAB = ∆NAB. Chứng minh đường thẳng AB là đường trung trực của đoạn thẳng MN.
Đề bài
Quan sát Hình 44 , biết ∆MAB = ∆NAB. Chứng minh đường thẳng AB là đường trung trực của đoạn thẳng MN.
Phương pháp giải - Xem chi tiết
A và B cùng cùng nằm trên đường trung trực của đoạn thẳng MN
Lời giải chi tiết
Vì ∆MAB = ∆NAB (giả thiết)
Suy ra AM = AN, BM = BN (các cặp cạnh tương ứng).
Do đó A và B cùng cách đều hai điểm M, N.
Suy ra A và B cùng nằm trên đường trung trực của đoạn thẳng MN.
Hay đường thẳng AB là đường trung trực của đoạn thẳng MN.
Vậy đường thẳng AB là đường trung trực của đoạn thẳng MN.
Cùng chủ đề:
Giải Bài 62 trang 87 sách bài tập toán 7 - Cánh diều