Giải bài 7 trang 67 vở thực hành Toán 8
Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC, B ở giữa M và C.
Đề bài
Cho tam giác ABC cân tại A; M là một điểm thuộc đường thẳng BC, B ở giữa M và C. Gọi E, K lần lượt là chân đường vuông góc hạ từ M và từ B xuống AC, còn N, D lần lượt là chân đường vuông góc hạ từ B xuống MEvà từ M xuống AB (H.3.46).
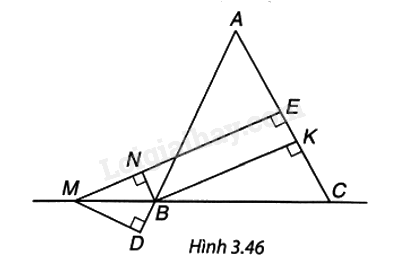
Chứng minh rằng:
a) Tứ giác BKEN là hình chữ nhật.
b) BK bằng hiệu khoảng cách từ M đến AC và đến AB (dù M thay đổi trên đường thẳng BC miễn là B nằm giữa M và C) tức là BK = ME – MD.
Phương pháp giải - Xem chi tiết
a) Chứng minh BKEN có ba góc vuông nên là hình chữ nhật.
b) Dựa vào tính chất của hình chữ nhật, tam giác cân, tam giác vuông để chứng minh.
Lời giải chi tiết
a) Tứ giác BKEN có ba góc vuông N, E, K nên là hình chữ nhật.
b) Tứ giác BKEN là hình chữ nhật nên NE = BK, BN // EK.
⇒ \(\widehat {NBM} = \widehat {KCB}\) (hai góc đồng vị). (1)
Ta có \(\widehat {MBD} = \widehat {CBK}\) (hai góc đối đỉnh). (2)
Theo giả thiết, tam giác ABC cân tại A ⇒ \(\widehat {ACB} = \widehat {ABC}\) (3).
Từ (1), (2), (3) suy ra \(\widehat {NBM} = \widehat {DBM}\)
Hai tam giác vuông NBM và DBM có: DB là cạnh chung, \(\widehat {NBM} = \widehat {DBM}\) (chứng minh trên) nên ∆NBM = ∆DBM (cạnh huyền – góc nhọn) ⇒ MN = MD.
Ta có ME – MD = ME – MN = NE = BK (điều phải chứng minh).