Giải các phương trình sau: A 2x - 3 = 5x - 2 + 8 b x — Không quảng cáo

Phương pháp giải

1. Đưa phương trình về dạng $ax + b = 0$ để giải.

2.

a) Lấy 2 điểm A, B thuộc đồ thị hàm số. Vẽ đường thẳng đi qua 2 điểm đó ta được đồ thị (d).

Tính diện tích tam giác OAB vuông tại O: ${S_{\Delta OAB}} = \frac{1}{2}OA.OB$.

b) Phương trình đường thẳng (d’) có dạng: $y = ax + b\left( {a \ne 0} \right)$

Hai đường thẳng $y = ax + b\left( {a \ne 0} \right)$ và $y = a'x + b'\left( {a' \ne 0} \right)$ song song nếu $a = a';b \ne b'$.

Tiếp theo thay tọa độ điểm $M\left( {1;5} \right)$ vào phương trình đường thẳng (d’) để tìm được phương trình.

1. a) $2\left( {x - 3} \right) = 5\left( {x - 2} \right) + 8$

$\begin{array}{l}2x - 6 = 5x - 10 + 8\\2x - 6 = 5x - 2\\2x - 5x =  - 2 + 6\\ - 3x = 4\\x =  - \frac{4}{3}\end{array}$

Vậy $x =  - \frac{4}{3}$

b) $\frac{{x - 1}}{9} + \frac{{x - 3}}{7} = 2$

$\begin{array}{l}\frac{{7\left( {x - 1} \right)}}{{63}} + \frac{{9\left( {x - 3} \right)}}{{63}} = \frac{{2.63}}{{63}}\\7\left( {x - 1} \right) + 9\left( {x - 3} \right) = 2.63\\7x - 7 + 9x - 27 = 126\\7x + 9x = 126 + 27 + 7\\16x = 160\\x = 10\end{array}$

Vậy $x = 10$

2. a) Cho $x = 0$ thì $y = 5$, ta được $B\left( {0;5} \right)$ là giao điểm của (d) với các trục tọa độ Oy.

Cho $y = 0$ thì $x = \frac{5}{2}$, ta được $A\left( {\frac{5}{2};0} \right)$ là giao điểm của (d) với các trục tọa độ Oy.

Đường thẳng AB chính là đồ thị (d).

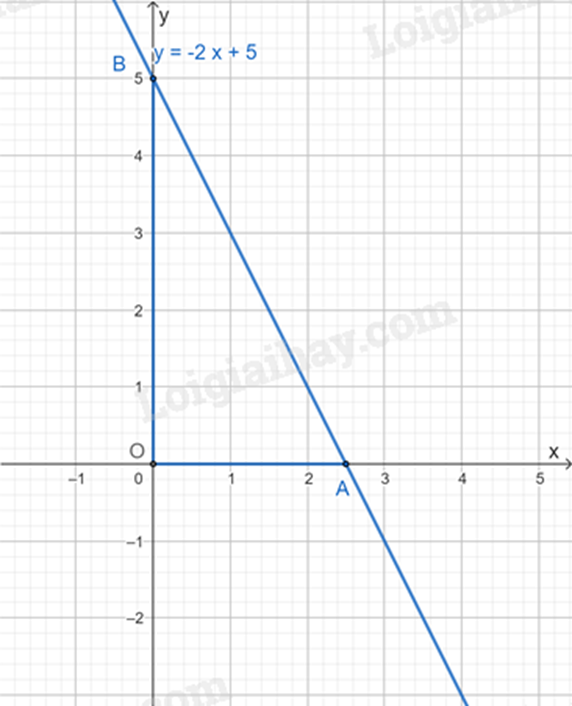
Vì A, B lần lượt là giao điểm của đường thẳng (d) và trục Ox, Oy nên $OA \bot OB$.

Suy ra $\Delta OAB$ vuông tại O.

Diện tích $\Delta OAB$ là: ${S_{\Delta OAB}} = \frac{1}{2}OA.OB = \frac{1}{2}\frac{5}{2}.5 = \frac{{25}}{4}$ (đơn vị diện tích).

b) Gọi phương trình (d’) cần tìm có dạng: $y = ax + b\left( {a \ne 0} \right)$.

Vì đường thẳng (d’) song song với (d) nên $a =  - 2,b \ne 5$, khi đó phương trình đường thẳng trở thành:

$y =  - 2x + b$

Điểm $M\left( {1;5} \right)$ thuộc đường thẳng (d’) nên ta có:

$\begin{array}{l}5 =  - 2.1 + b\\b = 5 + 2\\b = 7(TM)\end{array}$

Vậy phương trình đường thẳng cần tìm là $y =  - 2x + 7$.