Giải câu hỏi trang 95, 96 SGK Toán 9 tập 1 - Cùng khám phá
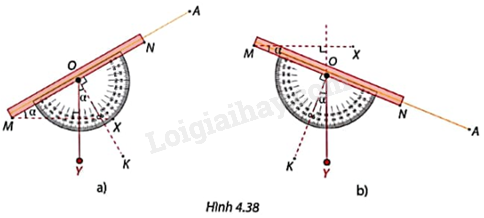
Khi sử dụng giác kế đứng, người ta đặt mắt ở vị trí M và hướng ống ngắm MN về phía điểm A cần quan sát như trong Hình 4.38. Góc AMX giữa hướng nhìn và phương ngang được gọi là góc nâng của A (so với M) nếu hướng nhìn xiên lên trên (Hình 4.38a) hoặc gọi là góc hạ của A (so với M) nếu hướng nhìn xiên xuống dưới (Hình 4.38b). Vì sao góc AMX luôn bằng góc KOY tạo bởi dây dọi và tia OK đi qua vạch \({90^o}\)?
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 95 SGK Toán 9 Cùng khám phá
Khi sử dụng giác kế đứng, người ta đặt mắt ở vị trí M và hướng ống ngắm MN về phía điểm A cần quan sát như trong Hình 4.38 . Góc AMX giữa hướng nhìn và phương ngang được gọi là góc nâng của A (so với M) nếu hướng nhìn xiên lên trên ( Hình 4.38a ) hoặc gọi là góc hạ của A (so với M) nếu hướng nhìn xiên xuống dưới ( Hình 4.38b ). Vì sao góc AMX luôn bằng góc KOY tạo bởi dây dọi và tia OK đi qua vạch \({90^o}\)?
Phương pháp giải:
Sử dụng tính chất của hai góc bù nhau để giải thích.
Lời giải chi tiết:
Trong Hình 4.38a:
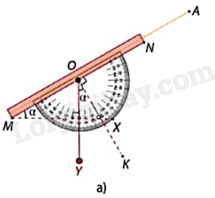
Ta có: \(\widehat {AMX} + \widehat {MOY} = \widehat {KOY} + \widehat {MOY}\left( { = {{90}^o}} \right)\) nên \(\widehat {AMX} = \widehat {KOY}\).
Trong Hình 4.38b: Gọi E là giao điểm của MX và đường thẳng OY.
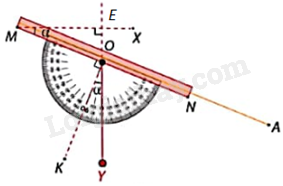
Ta có: \(\widehat {AMX} + \widehat {MOE} = {90^o}\), \(\widehat {KOY} + \widehat {YON} = {90^o}\), \(\widehat {MOE} = \widehat {YON}\) (hai góc đối đỉnh).
Do đó, \(\widehat {AMX} = \widehat {KOY}\).
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 96 SGK Toán 9 Cùng khám phá
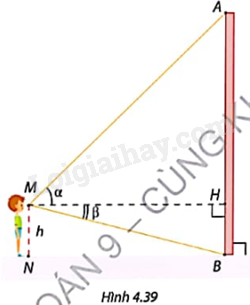
Học sinh thực hiện và trình bày tại lớp lời giải cho bài toán sau: Trong Hình 4.39, chiều cao từ mắt đến mặt đất của bạn học sinh là \(MN = h\left( m \right)\), góc nâng của đỉnh cột A là \(\alpha \) và góc hạ của chân cột B là \(\beta \). Giải thích vì sao \(AB = h\left( {1 + \frac{{\tan \alpha }}{{\tan \beta }}} \right)\).
Phương pháp giải:
+ Chứng minh tứ giác HBNM là hình chữ nhật, do đó \(HB = MN = h\).
+ Tam giác HBM vuông tại H nên \(HB = MH.\tan \beta \), suy ra \(MH = \frac{{HB}}{{\tan \beta }}\).
+ Tam giác MHA vuông tại H nên \(HA = MH.\tan \alpha = \frac{{HB}}{{\tan \beta }}.\tan \alpha \).
+ Kết hợp với \(AB = HA + HB\), từ đó suy ra điều phải chứng minh.
Lời giải chi tiết:
Tứ giác HBNM có: \(\widehat {MHB} = \widehat {HBN} = \widehat {MNB} = {90^o}\) nên tứ giác HBNM là hình chữ nhật, do đó \(HB = MN = h\).
Tam giác HBM vuông tại H nên \(HB = MH.\tan \beta \), suy ra \(MH = \frac{{HB}}{{\tan \beta }} = \frac{h}{{\tan \beta }}\).
Tam giác MHA vuông tại H nên
\(HA = MH.\tan \alpha = \frac{h}{{\tan \beta }}.\tan \alpha \).
Ta có:
\(AB = HA + HB = \frac{h}{{\tan \beta }}.\tan \alpha + h = h\left( {1 + \frac{{\tan \alpha }}{{\tan \beta }}} \right)\) (đpcm).
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 96 SGK Toán 9 Cùng khám phá
Đo chiều cao cột cờ
Học sinh thực hiện ngoài trời và trình bày kết quả trước cả lớp.
Sử dụng giác kế và thước để đo góc nâng \(\alpha \) của đỉnh cột cờ, góc hạ \(\beta \) của chân cột cờ và chiều cao h tính từ mắt bạn quan sát đến mặt đất.
Điền các kết quả đo được vào Bảng 4.4 và tính chiều cao cột AB bằng công thức có được từ hoạt động 2.
Thực hiện nhiều lần với các bạn khác nhau và vị trí quan sát khác nhau. So sánh các kết quả tính và nhận xét.

Phương pháp giải:
+ Thực hiện đo góc nâng \(\alpha \) của đỉnh cột cờ, góc hạ \(\beta \) của chân cột cờ và chiều cao h tính từ mắt bạn quan sát đến mặt đất.5/8/2024
+ Áp dụng công thức \(AB = h\left( {1 + \frac{{\tan \alpha }}{{\tan \beta }}} \right)\) để tính chiều cao cột cờ rồi điền vào bảng.
Lời giải chi tiết:

Các kết quả đo ở các lần là xấp xỉ nhau.