Giải mục 1 trang 15, 16 SGK Toán 10 tập 2 - Chân trời sáng tạo
Lời giải cho phương trình như sau đúng hai sai?
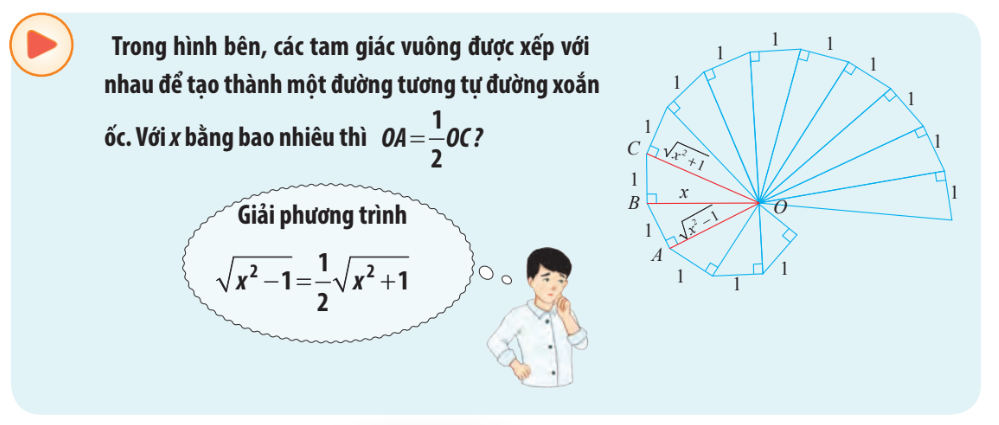
HĐ Khởi động
Phương pháp giải:
Bước 1: Bình phương hai vế làm mất căn bậc hai
Bước 2: Rút gọn và giải phương trình vừa tìm được
Bước 3: Thử lại nghiệm vừa tìm được và kết luận
Lời giải chi tiết:
Ta có điều kiện hiểu nhiên \(x > 0\)
\(\begin{array}{l}\sqrt {{x^2} - 1} = \frac{1}{2}\sqrt {{x^2} + 1} \\ \Rightarrow {x^2} - 1 = \frac{1}{4}\left( {{x^2} + 1} \right)\\ \Rightarrow \frac{3}{4}{x^2} - \frac{5}{4} = 0\end{array}\)
\( \Rightarrow x = \pm \sqrt {\frac{5}{3}} \)
Thử lại, kết hợp điều kiện của x ta thấy \(x = \sqrt {\frac{5}{3}} \) thỏa mãn phương trình.
Vậy khi \(x = \sqrt {\frac{5}{3}} \) thì \(OA = \frac{1}{2}OC\)
HĐ Khám phá 1
Lời giải cho phương trình \(\sqrt { - 2{x^2} - 2x + 11} = \sqrt { - {x^2} + 3} \) như sau đúng hai sai?
\(\)\(\sqrt { - 2{x^2} - 2x + 11} = \sqrt { - {x^2} + 3} \)
\( \Rightarrow - 2{x^2} - 2x + 11 = - {x^2} + 3\) (bình phương cả hai vế để làm mất dấu căn)
\( \Rightarrow {x^2} + 2x - 8 = 0\) (chuyển vế, rút gọn)
\( \Rightarrow x = 2\) hoặc \(x = - 4\) (giải phương trình bậc hai)
Vậy phương trình đã cho có hai nghiệm là 2 và -4
Lời giải chi tiết:
Thay \(x = 2\) vào phương trình \(\sqrt { - 2{x^2} - 2x + 11} = \sqrt { - {x^2} + 3} \) ta thấy không thỏa mãn vì dưới dấu căn là \( - 1\) không thỏa mãn
Vậy \(x = 2\) không là nghiệm của phương trình do đó lời giải như trên là sai.
Thực hành 1
Giải phương trình \(\sqrt {31{x^2} - 58x + 1} = \sqrt {10{x^2} - 11x - 19} \)
Phương pháp giải:
Bước 1: Bình phương hai vế của phương trình để làm mất dấu căn
Bước 2: Chuyển vế, rút gọn đưa về phương trình bậc hai một ẩn
Bước 3: Giải phương trình nhận được ở bước 2
Bước 4: Thử lại xem nghiệm đã tìm được ở bước 3 có thỏa mãn phương trình không và kết luận
Lời giải chi tiết:
Bình phương hai vế của phương trình đã cho, ta được:
\(\begin{array}{l}\sqrt {31{x^2} - 58x + 1} = \sqrt {10{x^2} - 11x - 19} \\ \Rightarrow 31{x^2} - 58x + 1 = 10{x^2} - 11x - 19\\ \Rightarrow 21{x^2} - 47x + 20 = 0\end{array}\)
\( \Rightarrow x = \frac{5}{3}\) hoặc \(x = \frac{4}{7}\)
Thay lần lượt các nghiệm trên vào phương trình đã cho, ta thấy không có nghiệm nào thỏa mãn
Vậy phương trình đã cho vô nghiệm
Chú ý khi giải : sau khi bình phương hai vế thì các bước giải tiếp theo chỉ được sử dụng dấu suy ra không được sử dụng dấu tương đương (vì tập nghiệm của chúng có thể không giống nhau)