Giải mục 1 trang 79, 80 SGK Toán 8 tập 2 - Kết nối tri thức
Trong hình 9.2, ΔABC và ΔABC là hai tam giác
HĐ1
Trong hình 9.2, ΔABC và ΔDEF là hai tam giác có các cạnh tương ứng song song và các góc tương ứng bằng nhau, tức là AB // DE, AC // DF, BC // EF và \(\widehat A = \widehat D{,^{}}\widehat B = \widehat E{;^{}}\widehat C = \widehat F\)
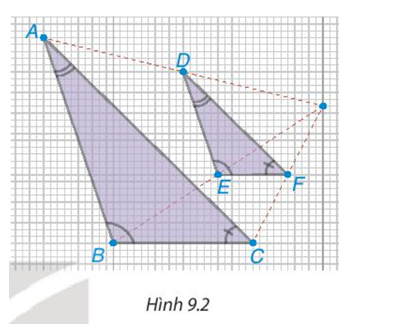
Nhìn hình vẽ, hãy cho biết giá trị các tỉ số sau: \(\frac{{AB}}{{DE}}{;^{}}\frac{{BC}}{{EF}}{;^{}}\frac{{AC}}{{DF}}\)
Phương pháp giải:
Quan sát hình vẽ để tính các tỉ số
Lời giải chi tiết:
Ta có: \(\frac{{AB}}{{DE}} = 2{;^{}}\frac{{BC}}{{EF}} = 2{;^{}}\frac{{AC}}{{DF}} = 2\)
LT1
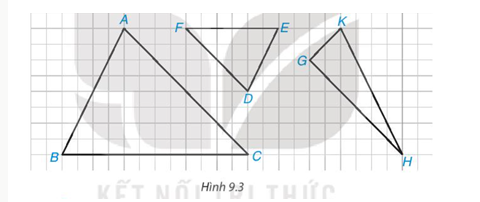
Trong các tam giác được vẽ trên ô lưới vuông, có một cặp tam giác đồng dạng. Hãy chỉ ra cặp tam giác đó, viết đúng kí hiệu đồng dạng và tìm tỉ số đồng dạng của chúng.
Phương pháp giải:
Quan sát hình vẽ để tìm hai tam giác đồng dạng và tỉ số của chúng
Lời giải chi tiết:
ΔABC \(\backsim\) ΔDEF với tỉ số đồng dạng là \(2\)
TTN
Cho \(\Delta ABC \backsim \Delta MNP\) . Chứng minh rằng:
a) Nếu tam giác ABC cân tại A thì tam giác MNP cân tại đỉnh M.
b) Nếu tam giác ABC đều thì tam giác MNP đều.
c) Nếu \(AB \ge AC \ge BC\) thì \(MN \ge MP \ge NP\)
Phương pháp giải:
Sử dụng \(\Delta ABC \backsim \Delta MNP\) nên \(\widehat A = \widehat M{;^{}}\widehat B = \widehat N{;^{}}\widehat C = \widehat P\)
Lời giải chi tiết:
a) Tam giác ABC tại A nên \(\widehat B = \widehat C\) (1)
Vì \(\Delta ABC \backsim \Delta MNP\) nên \(\widehat A = \widehat M{;^{}}\widehat B = \widehat N{;^{}}\widehat C = \widehat P\) (2)
Từ (1) và (2) nên \(\widehat N = \widehat P\) suy ra tam giác MNP cân tại M.
b) Vì tam giác ABC là tam giác đều nên \(\widehat A = \widehat B = \widehat C = {60^o}\) (3)
Vì \(\Delta ABC \backsim \Delta MNP\) nên \(\widehat A = \widehat M{;^{}}\widehat B = \widehat N{;^{}}\widehat C = \widehat P\) (4)
Từ (3) và (4) suy ra \(\widehat M = \widehat N = \widehat P = {60^o}\) nên tam giác MNP là tam giác đều.
c) Vì tam giác ABC có \(AB \ge AC \ge BC\) suy ra \(\widehat C \ge \widehat B \ge \widehat A\) (quan hệ giữa góc và cạnh đối điện) (5)
Mà \(\Delta ABC \backsim \Delta MNP\) nên \(\widehat A = \widehat M{;^{}}\widehat B = \widehat N{;^{}}\widehat C = \widehat P\) (6)
Từ (5) và (6) suy ra \(\widehat P \ge \widehat N \ge \widehat M\) nên \(MN \ge MP \ge NP\)