Giải mục 1 trang 80, 81 SGK Toán 7 tập 1 - Kết nối tri thức
Hãy nêu tên tất cả các tam giác cân trong Hình 4.59. Với mỗi tam cân đó, hãy nêu tên cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của chúng.
Câu hỏi
Hãy nêu tên tất cả các tam giác cân trong Hình 4.59. Với mỗi tam cân đó, hãy nêu tên cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của chúng.
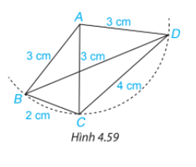
Phương pháp giải:
Tam giác cân là tam giác có hai cạnh bằng nhau. Hai cạnh bằng nhau đó gọi là 2 cạnh bên, cạnh còn lại của tam giác gọi là cạnh đáy.
Lời giải chi tiết:
+) Tam giác ABD cân tại đỉnh A có:
AB, AD là 2 cạnh bên
BD là cạnh đáy
\(\widehat B,\widehat D\) là 2 góc ở đáy
\(\widehat A\) là góc ở đỉnh
+) Tam giác ADC cân tại A có:
AC, AD là 2 cạnh bên
DC là cạnh đáy
\(\widehat C,\widehat D\) là 2 góc ở đáy
\(\widehat A\) là góc ở đỉnh
+) Tam giác ABC cân tại A có:
AB, AC là 2 cạnh bên
BC là cạnh đáy
\(\widehat C,\widehat B\) là 2 góc ở đáy
\(\widehat A\) là góc ở đỉnh
HĐ 1
Quan sát tam giác ABC cân tại A như Hình 4.60. Lấy D là trung điểm của đoạn thẳng BC.
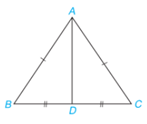
a) Chứng minh rằng \(\Delta \) ABD = \(\Delta \) ACD theo trường hợp cạnh - cạnh - cạnh.
b) Hai góc B và C của tam giác ABC có bằng nhau không?
Phương pháp giải:
a) Chứng minh ba cạnh của 2 tam giác trên bằng nhau
b) Từ câu a) suy ra 2 cặp góc tương ứng bằng nhau.
Lời giải chi tiết:
a) Xét hai tam giác ABD và ACD có:
AB=AC
AD chung
BD=DC
=>\(\Delta \)ABD = \(\Delta \)ACD (c.c.c)
b) Do \(\Delta \)ABD = \(\Delta \)ACD nên \(\widehat B = \widehat C\)( 2 góc tương ứng)
HĐ 2
Cho tam giác MNP có \(\widehat M = \widehat N\). Vẽ tia phân giác PK của tam giác \(MNP(K \in MN)\).
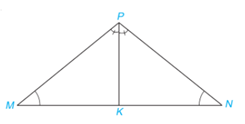
Chứng minh rằng:
a) \(\widehat {MKP} = \widehat {NKP}\);
b) \(\Delta MPK = \Delta NPK\);
c) Tam giác MNP có cân tại \(P\) không?
Phương pháp giải:
a) Sử dụng định lí: Tổng 3 góc trong một tam giác bằng 180 độ
b) Chứng minh 2 tam giác bằng nhau theo trường hợp góc – cạnh - góc
c) Sử dụng định nghĩa tam giác cân: Tam giác MNP cân là tam giác có 2 cạnh bằng nhau
Lời giải chi tiết:
a)
Xét tam giác MPK có:
\(\widehat {PKM} + \widehat {MPK} + \widehat {KMP} = {180^o}\)
Xét tam giác NPK có:
\(\widehat {PKN} + \widehat {NPK} + \widehat {KNP} = {180^o}\)
Mà \(\widehat {KMP} = \widehat {KNP};\,\,\,\widehat {MPK} = \widehat {NPK}\)
Suy ra \(\widehat {MKP} = \widehat {NKP}\).
b)Xét hai tam giác MPK và NPK có:
\(\widehat {MPK} = \widehat {NPK}\)
PK chung
\(\widehat {MKP} = \widehat {NKP}\)
=>\(\Delta MPK = \Delta NPK\)(g.c.g)
c) Do \(\Delta MPK = \Delta NPK\) nên MP=NP (2 cạnh tương ứng)
=> Tam giác MNP cân tại P.
Luyện tập 1
Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62.
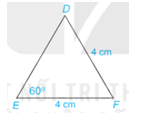
Phương pháp giải:
Chứng minh tam giác DEF cân tại F từ đó suy ra số đo các góc.
Lời giải chi tiết:
Cách 1: Vì tam giác DEF có DF=FE(=4cm) nên tam giác DEF cân tại F.
Mà \(\widehat E=60^0\)
Do đó, \(\Delta DEF \) đều. (Tam giác cân có 1 góc bằng \(60^0\))
\(\Rightarrow \widehat D = \widehat F=\widehat E=60^0\).
Vì tam giác DEF đều nên DE = DF = FE = 4cm.
Cách 2: Xét tam giác DEF có DF=FE(=4cm) nên tam giác DEF cân tại F.
Suy ra \(\widehat E = \widehat D = {60^o}\) ( tính chất tam giác cân)
Áp dụng định lí tổng ba góc trong tam giác vào tam giác DEF, ta có:
\(\begin{array}{l}\widehat D + \widehat E + \widehat F = {180^o}\\ \Rightarrow {60^o} + {60^o} + \widehat F = {180^o}\\ \Rightarrow \widehat F = {60^o}\end{array}\)
Vì tam giác DEF đều nên DE = DF = FE = 4cm.
TTN
Thử thách nhỏ
Một tam giác có gì đặc biệt nếu thoả mãn một trong các điều kiện sau:
a) Tam giác có ba góc bằng nhau?
b) Tam giác cân có một góc bằng 60°?
Phương pháp giải:
Áp dụng: Tam giác đều là tam giác có 3 cạnh bằng nhau hoặc ba góc bằng nhau.
Lời giải chi tiết:
a) Tam giác có ba góc bằng nhau là tam giác đều
b) Tam giác cân có 1 góc bằng 60 độ là tam giác đều.