Giải mục 2 trang 45, 46 SGK Toán 7 tập 2 - Chân trời sáng tạo
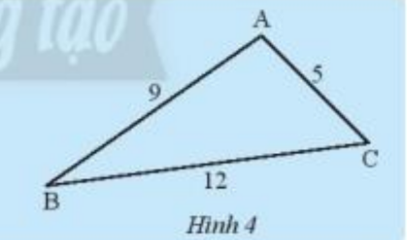
Hãy so sánh tổng độ dài hai cạnh của tam giác trong Hình 4 với độ dài cạnh còn lại.
HĐ 2
Hãy so sánh tổng độ dài hai cạnh của tam giác trong Hình 4 với độ dài cạnh còn lại.
Phương pháp giải:
Ta so sánh tổng 2 cạnh trong tam giác với cạnh còn lại.
Lời giải chi tiết:
Trong tam giác ABC, xét tổng độ dài 2 cạnh so với cạnh còn lại :
\(\begin{array}{l}AB + AC = 9 + 5 > BC = 12\\AB + BC = 9 + 12 > AC = 5\\AC + BC = 12 + 5 > AB = 9\end{array}\)
Vậy tổng độ dài 2 cạnh trong 1 tam giác luôn lớn hơn độ dài cạnh còn lại .
Thực hành 2
Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của tam giác?
a) 7cm; 8cm; 11cm
b) 7cm; 9cm; 16cm
c) 8cm; 9cm; 16cm
Phương pháp giải:
So sánh độ dài cạnh lớn nhất với tổng độ dài 2 cạnh còn lại
Lời giải chi tiết:
a) Vì 7 + 8 > 11
Nên a là một tam giác theo bất đẳng thức tam giác
b) Vì 7 + 9 = 16 không thỏa mãn bất đẳng thức tam giác nên b không phải là tam giác
c) Vì 8 + 9 > 16
Nên c là một tam giác theo bất đẳng thức tam giác
Vận dụng
Cho tam giác ABC với độ dài ba cạnh là ba số nguyên. Nếu biết AB = 5cm AC = 3cm thì cạnh BC có thể có độ dài là bao nhiêu xăngtimét?
Phương pháp giải:
Sử dụng bất đẳng thức tam giác: Trong một tam giác, độ dài của một cạnh luôn nhỏ hơn tổng độ dài hai cạnh còn lại và lớn hơn hiệu độ dài 2 cạnh còn lại: b – c < a < b + c ( với a, b, c là độ dài 3 cạnh của tam giác)
Kết hợp điều kiện độ dài cạnh BC là số nguyên
Lời giải chi tiết:
Áp dụng bất đẳng thức tam giác trong tam giác ABC, ta có:
5 - 3 < BC < 5 + 3
2 < BC < 8
Mà BC là số nguyên
\(\Rightarrow BC \in\) {3;4;5;6;7} cm
Vậy độ dài BC có thể là 3 cm, 4 cm, 5 cm, 6 cm hoặc 7 cm.