Giải mục 2 trang 89, 90 SGK Toán 9 tập 1 - Kết nối tri thức — Không quảng cáo

CH

Trả lời câu hỏi Câu hỏi trang 89 SGK Toán 9 Kết nối tri thức

Tại sao số đo cung lớn của một đường tròn luôn lớn hơn ${180^0}$

Phương pháp giải:

Dựa vào tổng số đo của cung nhỏ và cung lớn trên cùng một đường tròn bằng 360 độ.

Lời giải chi tiết:

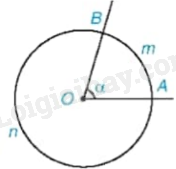
Xét đường tròn tâm O có cung AB nhỏ và cung AB lớn nên ta có

Sđ $\overset\frown{AB}$ nhỏ + sđ $\overset\frown{AB}$ lớn $={{360}^{0}}$

Và sđ $\overset\frown{AB}$ lớn >  sđ $\overset\frown{AB}$ nhỏ

Nên sđ $\overset\frown{AB}$ lớn + sđ $\overset\frown{AB}$ lớn >  sđ $\overset\frown{AB}$ nhỏ + sđ $\overset\frown{AB}$ lớn

2 . sđ $\overset\frown{AB}$ lớn > ${{360}^{0}}$

sđ $\overset\frown{AB}$ lớn > ${{180}^{0}}$

Nên số đo cung lớn luôn lớn hơn 180 độ.

LT2

Trả lời câu hỏi Luyện tập 2 trang 90 S GK Toán 9 Kết nối tri thức

Cho điểm C nằm trên đường tròn (O). Đường trung trực của đoạn OC cắt (O) tại A. Tính số đo của các cung $\overset\frown{ACB}$ và $\overset\frown{ABC}$.

Phương pháp giải:

- Tính số đo các góc OCA và OCB, từ đó suy ra số đo cung $\overset\frown{AC}$, $\overset\frown{BC}$ và $\overset\frown{ACB}$.

-$\overset\frown{ABC}$ là cung lớn có chung hai mút A, C với cung nhỏ $\overset\frown{AC}$ nên sđ $\overset\frown{ABC}=360{}^\circ -$ sđ$\overset\frown{AC}$

Lời giải chi tiết:

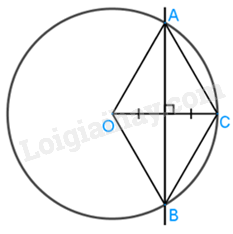
AB là đường trung trực của AB của OC nên AC = OA (tính chất đường trung trực)

mà OA = OC = R nên AC = OA = OC

hay $\Delta \,ACO$ là tam giác đều.

Do đó: $\widehat{AOC}=60{}^\circ$ (tính chất của tam giác đều) $\Rightarrow$ sđ $\overset\frown{AC}=60{}^\circ$

Tương tự ta có: sđ $\overset\frown{BC}=60{}^\circ$

Suy ra:

sđ $\overset\frown{ACB}=$sđ $\overset\frown{AC}$ + sđ $\overset\frown{BC}=60{}^\circ +60{}^\circ =120{}^\circ$

$\overset\frown{ABC}$ là cung lớn có chung hai mút A, C với cung nhỏ $\overset\frown{AC}$

nên sđ $\overset\frown{ABC}=360{}^\circ -$ sđ$\overset\frown{AC}=360{}^\circ -60{}^\circ =300{}^\circ$