Giải mục 3 trang 12, 13 SGK Toán 8 - Cùng khám phá
Giải thích vì sao ta có thể viết:
Hoạt động 3
Giải thích vì sao ta có thể viết:
\(\left( {x + 2y} \right).\left( {2x - y} \right) = x.2x + y.\left( { - y} \right) + 2y.2x + 2y.\left( { - y} \right) = 2{x^2} - xy + 4xy - 2{y^2} = 2{x^2} + 3xy - 2{y^2}\)
Phương pháp giải:
Sử dụng phương pháp nhân đơn thức với đa thức: ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các kết quả lại với nhau.
Lời giải chi tiết:
Đặt \(A = x + 2x\) ta có \(\left( {x + 2y} \right)\left( {2x - y} \right) = A.\left( {2x - y} \right) = A.2x - A.y\)
Từ đây ta có \(\left( {x + 2y} \right)\left( {2x - y} \right) = \left( {x + 2y} \right).2x - \left( {x + 2y} \right).y\)
\( = x.2x + y.\left( { - y} \right) + 2y.2x + 2y.\left( { - y} \right) = 2{x^2} - xy + 4xy - 2{y^2} = 2{x^2} + 3xy - 2{y^2}\)
Vậy ta có thể viết \(\left( {x + 2y} \right).\left( {2x - y} \right) = x.2x + y.\left( { - y} \right) + 2y.2x + 2y.\left( { - y} \right) = 2{x^2} - xy + 4xy - 2{y^2} = 2{x^2} + 3xy - 2{y^2}\)
Luyện tập 3
Tính tích của hai đa thức \(G = {x^2} - 3y + 8\) và \(H = {y^2} - 2x\)
Phương pháp giải:
Sử dụng phương pháp nhân đa thức với đa thức: ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các kết quả lại với nhau.
Lời giải chi tiết:
Ta có
\(\begin{array}{l}G.H = \left( {{x^2} - 3y + 8} \right).\left( {{y^2} - 2x} \right)\\ = {x^2}.\left( {{y^2} - 2x} \right) - 3y.\left( {{y^2} - 2x} \right) + 8.\left( {{y^2} - 2x} \right)\\ = {x^2}{y^2} - 2{x^3} - 3{y^3} + 6xy + 8{y^2} - 16x\end{array}\)
Vận dụng
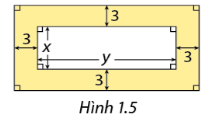
Trong phần Khởi động, hãy tính diện tích của phần được tô màu trong Hình 1.5 theo \(x\) và \(y\).
Phương pháp giải:
Viết biểu thức biểu diễn diện tích phần tô màu là hiệu của 2 hình chữ nhật có kích thước như hình vẽ.
Lời giải chi tiết:
Theo hình 1.5, hình chữ nhật lớn có chiều dài và chiều rộng lần lượt là: \(y + 6\) và \(x + 6\)
Diện tích phần tô màu là :
\(\left( {x + 6} \right).\left( {y + 6} \right) - xy = xy + 6x + 6y + 36 - xy = 6x + 6y + 36\)
Vậy diện tích phần được tô màu là \(6x + 6y + 36\).