Giải mục 3 trang 71, 72 SGK Toán 9 tập 1 - Kết nối tri thức — Không quảng cáo

LT4

Trả lời câu hỏi Luyện tập 4 trang 71 SGK Toán 9 Kết nối tri thức

Sử dụng MTCT tính các ti số lượng giác và làm tròn kết quả đến chữ số thập phân thứ ba:

a) $\sin {40^0}54';$

b) $\cos {52^0}15';$

c) $\tan {69^0}36'$

d) $\cot {25^0}18'$

Phương pháp giải:

Để tính $\sin {40^0}54'$ ta bấm:

Tương tự với cos và tan.

Tuy nhiên đối với cot thì ta có thể làm như sau: $\cot {25^0}18' = \frac{1}{{\tan {{25}^0}18'}}$ hoặc sử dụng tính chất hai góc phụ nhau có tan bằng cot.

Lời giải chi tiết:

a) $\sin {40^0}54';$

Ta có: $\sin {40^0}54' = 0,6547408137 \approx 0,655$

b) $\cos {52^0}15';$

Ta có: $\cos {52^0}15' = 0,61221728 \approx 0,612$

c) $\tan {69^0}36'$

Ta có: $\tan {69^0}36' = 2,688918967 \approx 2,689$

d) $\cot {25^0}18'$

Ta có: $\tan {25^0}18' = 0,4726978344$ nên $\cot {25^0}18' = \frac{1}{{\tan {{25}^0}18'}} = 2,115516356 \approx 2,116$

LT5

Trả lời câu hỏi Luyện tập 5 trang 72 SGK Toán 9 Kết nối tri thức

Dùng MTCT, tìm các góc $\alpha$ (làm tròn đến phút) , biết:

a) $\sin \alpha  = 0,3782;$

b) $\cos \alpha  = 0,6251;$

c) $\tan \alpha  = 2,154;$

d) $\cot \alpha  = 3,253.$

Phương pháp giải:

Để tìm góc $\alpha$ khi biết $\sin \alpha  = 0,3782$ thì ta bấm MTCT:

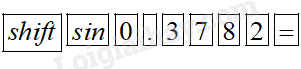
ta được kết quả 22,222231 thì ta bấm tiếp ⁰ ’’’ ta được kết quả ${22^0}13'20.03'' \approx {22^0}13'$ tương tự đối với trường hợp cos và tan. Tuy nhiên đối với trường hợp tìm $\alpha$ khi biết $\cot \alpha$ thì ta có thể tìm góc ${90^0} - \alpha$ (vì $\tan \left( {{{90}^0} - \alpha } \right) = \cot \alpha$ từ đó ta tính được $\alpha$) .

Lời giải chi tiết:

a) $\sin \alpha  = 0,3782;$

Ta có: $\sin \alpha  = 0,3782$ nên $\alpha  = {22^0}13'20,03'' \approx {22^0}13'$

b) $\cos \alpha  = 0,6251;$

Ta có: $\cos \alpha  = 0,6251$ nên $\alpha  = {51^0}18'37,7 \approx {51^0}19'$

c) $\tan \alpha  = 2,154;$

Ta có: $\tan \alpha  = 2,154$ nên $\alpha  = {65^0}5'48,46'' \approx {65^0}6'$

d) $\cot \alpha  = 3,253.$

Ta có: $\cot \alpha  = 3,253$ nên ${90^0} - \alpha  = {72^0}54'43,65'' \approx {72^0}55'$

Do đó $\alpha  \approx {90^0} - {72^0}55' = {17^0}5'$

VD

Trả lời câu hỏi Vận dụng trang 72 SGK Toán 9 Kết nối tri thức

Trở lại bài toán ở tình huống mở đầu: Trong một toàn chung cư, biết đoạn dốc vào sảnh toàn nhà dài 4 m, độ cao của đỉnh dốc bằng 0,4 m.

a) Hãy tính góc dốc.

b) Hỏi góc đó có đúng tiêu chuẩn của dốc cho người đi xe lăn không?

Tình huống mở đầu:

Ta có thể xác định “góc dốc” $\alpha$ của một đoạn đường dốc khi biết độ dài của dốc là a và độ cao của đỉnh dốc so với đường nằm ngang là h không? (H.4.1)

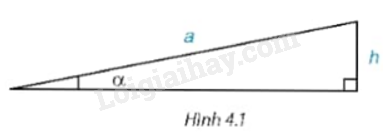
(Trong các tòa chung cư, người ta thường thiết kế đoạn dốc cho người đi xe lăn với góc dốc bé hơn ${6^0}$) .

Phương pháp giải:

Với con dốc ta biết chiều cao (cạnh đối) và chiều dài sảnh dốc (cạnh huyền) của tam giác vuông có góc nhọn $\alpha$, để tính $\alpha$ thì ta dùng tỉ số lượng giác $\sin \alpha$

Lời giải chi tiết:

a) Ta có: $\sin \alpha  = \frac{h}{a} = \frac{{0,4}}{4} = 0,1$, do đó $\alpha  \approx {5^0}44'.$

b) $\alpha  \approx {5^0}44' < 6^0$

Vậy góc đó đúng tiêu chuẩn cho người đi xe lăn.

TL

Trả lời câu hỏi Tranh luận trang 72 SGK Toán 9 Kết nối tri thức

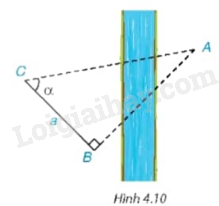
Để tính khoảng cách giữa hai địa điểm A, B không đo trực tiếp được, chẳng hạn A và B là hai địa điểm ở hai bên sông, người ta lấy điểm C về phía bờ sông có chứa B sao cho tam giác ABC vuông tại B. Ở bên bờ sông chứa B, người ta đo được $\widehat {ACB} = \alpha$ và $BC = a$ (H.4.10) . Với các dữ liệu đó, đã tính được khoảng cách AB chưa? Nếu được, hãy tính AB, biết $\alpha  = {55^0},a = 70$ m.

Phương pháp giải:

Tam giác ABC vuông tại B biết số đo góc $\alpha$ và cạnh kề BC, cần tính cạnh AB (cạnh đối) do đó ta dùng tỉ số lượng giác $\tan \alpha$

Lời giải chi tiết:

Ta có: $\tan \alpha  = \frac{{AB}}{{BC}}$ hay $\tan {55^0} = \frac{{AB}}{{70}}$ suy ra $AB = 70.\tan {55^0} \approx 99,97$ m.

Vậy khoảng cách AB khoảng 99,97 m.