Giải mục 3 trang 85, 86 SGK Toán 9 tập 1 - Cánh diều
Tìm độ dài cạnh góc vuông (AC) và số đo các góc nhọn (B,C) của tam giác vuông (ABC), biết cạnh góc vuông (AB = 5cm) và cạnh huyền (BC = 13cm).
LT4
Trả lời câu hỏi Luyện tập 4 trang 85 SGK Toán 9 Cánh diều
Tìm độ dài cạnh góc vuông \(AC\) và số đo các góc nhọn \(B,C\) của tam giác vuông \(ABC\), biết cạnh góc vuông \(AB = 5cm\) và cạnh huyền \(BC = 13cm\).
Phương pháp giải:
Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán.
Lời giải chi tiết:
Xét tam giác \(ABC\) vuông tại \(A\), ta có:
+) \(B{C^2} = A{B^2} + A{C^2}\) (theo định lý Pythagore), suy ra \({13^2} = {5^2} + A{C^2}\) hay \(AC = 12\left( {cm} \right)\).
+) \(\cos B = \frac{{AB}}{{BC}} = \frac{5}{{13}}\) suy ra \(\widehat B \approx 67^\circ \).
+) \(\widehat B + \widehat C = 90^\circ \) (tổng hai góc nhọn của tam giác vuông), suy ra \(\widehat C = 90^\circ - \widehat B \approx 90^\circ - 67^\circ = 23^\circ \).
LT5
Trả lời câu hỏi Luyện tập 5 trang 85 SGK Toán 9 Cánh diều
Tìm số đo góc nhọn \(C\) và độ dài cạnh góc vuông \(AB\), cạnh huyền \(BC\) của tam giác vuông \(ABC\), biết cạnh góc vuông \(AC = 7cm\) và \(\widehat B = 55^\circ \).
Phương pháp giải:
Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán.
Lời giải chi tiết:
Xét tam giác \(ABC\) vuông tại \(A\), ta có:
+) \(\widehat B + \widehat C = 90^\circ \) (tổng hai góc nhọn của tam giác vuông), suy ra \(\widehat C = 90^\circ - \widehat B = 90^\circ - 55^\circ = 35^\circ \).
+) \(AB = AC.\tan C = 7.\tan 35^\circ \approx 4,9\left( {cm} \right)\).
+) Ta có: \(AC = BC.\sin B\)
suy ra \(BC = \frac{AC}{\sin B} = \frac{7}{\sin 55^\circ} \approx 8,5\left( {cm} \right)\).
LT6
Trả lời câu hỏi Luyện tập 6 trang 86 SGK Toán 9 Cánh diều
Cho hình chữ nhật \(ABCD\) thỏa mãn \(AC = 6cm,\widehat {BAC} = 47^\circ \). Tính độ dài các đoạn thẳng \(AB,AD\).
Phương pháp giải:
Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán.
Lời giải chi tiết:
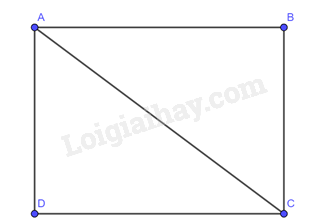
Xét tam giác \(ABC\) vuông tại \(B\) có:
+) \(AB = AC.\cos \widehat {BAC} = 6.\cos 47^\circ \approx 4,1\left( {cm} \right)\).
+) \(BC = AC.\sin \widehat {BAC} = 6.\sin 47^\circ \approx 4,4\left( {cm} \right)\).
Do \(ABCD\) là hình chữ nhật nên \(BC = AD\) (tính chất hình chữ nhật) suy ra \(AD \approx 4,4\left( {cm} \right)\).