Giải mục 4 trang 56, 57 SGK Toán 10 tập 2 - Chân trời sáng tạo — Không quảng cáo

HĐ Khám phá 7

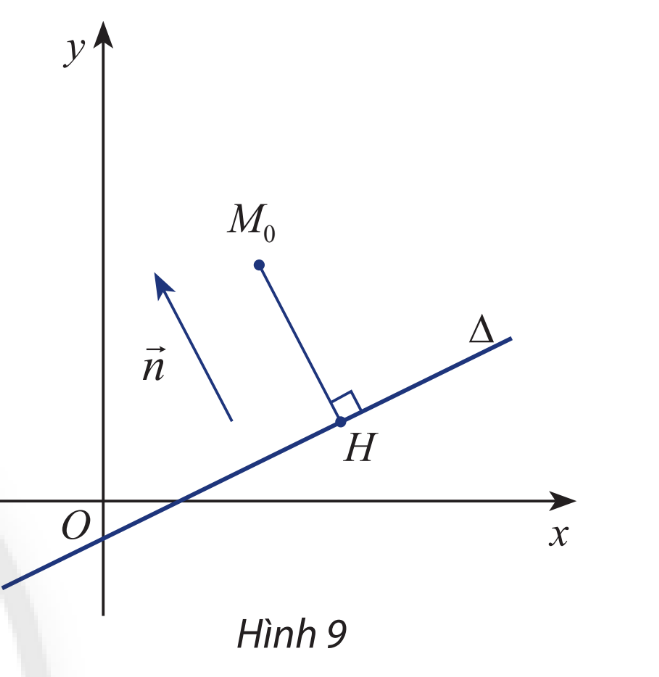
Trong mặt phẳng Oxy . Cho đường thẳng $\Delta :ax + by + c = 0\left( {{a^2} + {b^2} > 0} \right)$ có vectơ pháp tuyến $\overrightarrow n$ và cho điểm ${M_0}\left( {{x_0};{y_0}} \right)$có hình chiếu vuông góc $H\left( {{x_H};{y_H}} \right)$trên $\Delta$(hình 9).

a)  Chứng minh rằng hai vectơ $\overrightarrow n$ và $\overrightarrow {H{M_0}}$cùng phương và tìm tọa độ của chúng

b) Gọi p là tích vô hướng của hai vectơ $\overrightarrow n$ và $\overrightarrow {H{M_0}}$.

Chứng minh rằng $p = a{x_0} + b{y_0} + c$

c) Giải thích công thức $\left| {\overrightarrow {H{M_0}} } \right| = \frac{{\left| p \right|}}{{\left| {\overrightarrow n } \right|}}$

Phương pháp giải:

a) So sánh phương với vectơ chỉ phương

b)  Bước 1: Nhân tích vô hướng của hai vectơ

Bước 2: Thay tọa độ điẻm H vào đường thẳng tìm mối liên hệ

c) Thay vào công thức kết quả đã tìm được ở câu b)

Lời giải chi tiết:

a) Ta có: $\overrightarrow n$ và $\overrightarrow {H{M_0}}  = \left( {{x_0} - {x_H};{y_0} - {y_H}} \right)$

Mà H là hình chiếu vuông góc của ${M_0}$ trên $\Delta$ nên $H{M_0} \bot \Delta$

Mặt khác vectơ pháp tuyến $\overrightarrow n$ cùng vuông góc với $\Delta$

Suy ra $\overrightarrow n$ và $\overrightarrow {H{M_0}}$cùng phương (đpcm)

b) Ta có: $\overrightarrow n  = (a;b)$ và $\overrightarrow {H{M_0}}  = \left( {{x_0} - {x_H};{y_0} - {y_H}} \right)$

Suy ra $p = \overrightarrow n .\overrightarrow {H{M_0}}  = a\left( {{x_0} - {x_H}} \right) + b\left( {{y_0} - {y_H}} \right) = a{x_0} + b{y_0} - \left( {a{x_H} + b{y_H}} \right)$                (1)

Mà H thuộc đường thẳng $\Delta$ nên tọa độ điểm H thỏa mãn phương trình đường thẳng $\Delta$

Thay tọa độ điểm H vào phương trình $\Delta :ax + by + c = 0\left( {{a^2} + {b^2} > 0} \right)$ ta có:

$a{x_H} + b{y_H} + c = 0 \Leftrightarrow c =  - \left( {a{x_H} + b{y_H}} \right)$

Thay $c =  - \left( {a{x_H} + b{y_H}} \right)$ vào (1) ta có

$p = a{x_0} + b{y_0} + c$       (đpcm)

c) Ta có: $p = \overrightarrow n .\overrightarrow {H{M_0}}  \Leftrightarrow \overrightarrow {H{M_0}}  = \frac{p}{{\overrightarrow n }} \Rightarrow \left| {\overrightarrow {H{M_0}} } \right| = \left| {\frac{p}{{\overrightarrow n }}} \right| \Rightarrow \left| {\overrightarrow {H{M_0}} } \right| = \frac{{\left| p \right|}}{{\left| {\overrightarrow n } \right|}}$

Thực hành 6

Trong mặt phẳng Oxy , cho tam giác ABC có tọa độ các đỉnh là $A(1;1),B(5;2),C(4;4)$. Tính độ dài các đường cao của tam giác ABC

Phương pháp giải:

Bước 1: Viết phương trình tổng quat của các đường thẳng AB, AC, BC

Bước 2: Đường của kẻ từ A chính là khoảng cách từ điểm A đến đường thẳng BC (tương tự các đường cao còn lại)

Lời giải chi tiết:

Ta có: $\overrightarrow {AB}  = \left( {4;1} \right),\overrightarrow {AC}  = \left( {3;3} \right),\overrightarrow {BC}  = \left( { - 1;2} \right)$

+) Đường thẳng AB nhận vectơ $\overrightarrow {AB}  = \left( {4;1} \right)$làm phương trình chỉ phương nên có vectơ pháp tuyến là $\overrightarrow {{n_1}}  = \left( {1; - 4} \right)$ và đi qua điểm $A(1;1)$, suy ra ta có phương trình tổng quát của đường thẳng AB là:

$\left( {x - 1} \right) - 4\left( {y - 1} \right) = 0 \Leftrightarrow x - 4y + 3 = 0$

Độ dài đường cao kẻ từ C chính là khoảng cách từ điểm C đến đường thẳng AB

$d\left( {C,AB} \right) = \frac{{\left| {4 - 4.4 + 3} \right|}}{{\sqrt {{1^2} + {4^2}} }} = \frac{{9\sqrt {17} }}{{17}}$

+) Đường thẳng BC nhận vectơ $\overrightarrow {BC}  = \left( { - 1;2} \right)$làm phương trình chỉ phương nên có vectơ pháp tuyến là $\overrightarrow {{n_2}}  = \left( {2;1} \right)$ và đi qua điểm $B(5;2)$, suy ra ta có phương trình tổng quát của đường thẳng BC là:

$2\left( {x - 5} \right) + \left( {y - 2} \right) = 0 \Leftrightarrow 2x + y - 12 = 0$

Độ dài đường cao kẻ từ A chính là khoảng cách từ điểm A đến đường thẳng BC

$d\left( {A,BC} \right) = \frac{{\left| {2.1 + 1 - 12} \right|}}{{\sqrt {{2^2} + {1^2}} }} = \frac{{9\sqrt 5 }}{5}$

+) Đường thẳng AC nhận vectơ $\overrightarrow {AC}  = \left( {3;3} \right)$làm phương trình chỉ phương nên có vectơ pháp tuyến là $\overrightarrow {{n_3}}  = \left( {1; - 1} \right)$ và đi qua điểm $A(1;1)$, suy ra ta có phương trình tổng quát của đường thẳng AC là:

$\left( {x - 1} \right) - \left( {y - 1} \right) = 0 \Leftrightarrow x - y = 0$

Độ dài đường cao kẻ từ B chính là khoảng cách từ điểm B đến đường thẳng AC

$d\left( {B,AC} \right) = \frac{{\left| {5 - 2} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \frac{{3\sqrt 2 }}{2}$

Vận dụng 6

Tính khoảng cách giữa hai đường thẳng ${d_1}:4x - 3y + 2 = 0$ và ${d_2}:4x - 3y + 12 = 0$

Phương pháp giải:

Khoảng cách giữa hai đường thẳng song song là khoảng cách một điềm bất kì từ đường thẳng này tới đường thẳng còn lại

Lời giải chi tiết:

Ta thấy hai đường thẳng này song song, nên khoảng cách giữa chúng là khoảng cách từ một điểm bất kì từ đường thẳng này tới đường thẳng kia

Chọn điểm $A\left( {0;4} \right) \in {d_2}$, suy ra $d\left( {{d_1},{d_2}} \right) = d\left( {A,{d_1}} \right) = \frac{{\left| {4.0 - 3.4 + 2} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 2$

Vậy khoảng cách giữa hai đường thẳng ${d_1}:4x - 3y + 2 = 0$ và ${d_2}:4x - 3y + 12 = 0$ là 2