Giải mục 6 trang 21, 22 Chuyên đề học tập Toán 11 - Cánh diều
Trong Hình 34, cho đoạn thẳng AB. Nêu cách dựng:
Hoạt động 16
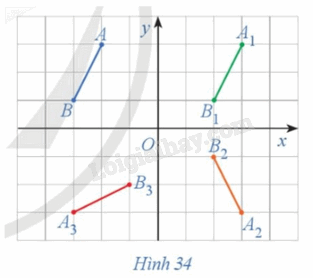
Trong Hình 34 , cho đoạn thẳng AB. Nêu cách dựng:
a) Đoạn thẳng A 1 B 1 là ảnh của đoạn thẳng AB qua phép tịnh tiến theo vectơ \(\vec u = \left( {5;\,0} \right)\);
b) Đoạn thẳng A 2 B 2 là ảnh của đoạn thẳng A 1 B 1 qua phép đối xứng trục Ox;
c) Đoạn thẳng A 3 B 3 là ảnh của đoạn thẳng A 2 B 2 qua phép quay tâm O với góc quay \(\;\varphi = --90^\circ ;\)
d) So sánh độ dài các đoạn thẳng \(AB,{\rm{ }}{A_1}{B_1},{\rm{ }}{A_2}{B_2},{\rm{ }}{A_3}{B_3}.\)
Phương pháp giải:
Quan sát hình 34 và dựa vào định nghĩa:
Cho vectơ \(\overrightarrow u \), phép tịnh tiến theo vectơ \(\overrightarrow u \) là phép biến hình biến điểm M thành điểm M’ sao cho \(\overrightarrow {MM'} = \overrightarrow u \).
Lời giải chi tiết:
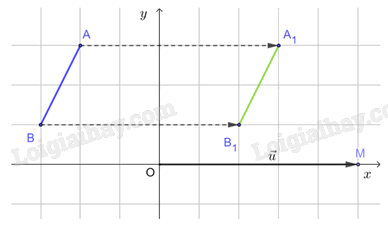
a) Lấy điểm M, sao cho M(5; 0). Khi đó \(\overrightarrow {OM} = \left( {5;\,0} \right) = \vec u\).
Lấy các điểm A 1 và B 1 sao cho \(\overrightarrow {A{A_1}} = \overrightarrow {OM} ,\,\overrightarrow {B{B_1}} = \overrightarrow {OM} \). Khi đó \(\overrightarrow {{\rm{A}}{{\rm{A}}_1}} = \overrightarrow {B{B_1}} = \vec u\) nên A 1 , B 1 lần lượt là ảnh của A, B qua phép tịnh tiến theo vectơ \(\vec u = \left( {5;\,0} \right)\). Vậy đoạn thẳng A 1 B 1 là ảnh của đoạn thẳng AB qua phép tịnh tiến theo vectơ \(\vec u = \left( {5;\,0} \right)\).
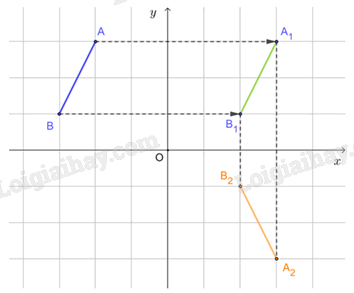
b) Từ A 1 , kẻ đường thẳng vuông góc với Ox, trên đường thẳng này lấy A 2 khác phía với A 1 đối với Ox sao cho khoảng cách từ A 1 đến Ox bằng khoảng cách từ A 2 tới Ox. Khi đó Ox là đường trung trực của đoạn thẳng A 1 A 2 .
Tương tự, dựng B 2 sao cho Ox là đường trung trực của đoạn thẳng B 1 B 2 .
Khi đó ta có phép đối xứng trục Ox biến các điểm A 1 , B 1 tương ứng thành các điểm A 2 , B 2 . Vậy đoạn thẳng A 2 B 2 là ảnh của đoạn thẳng A 1 B 1 qua phép đối xứng trục Ox.
c) Phép quay với góc quay – 90° có chiều quay cùng chiều kim đồng hồ.
Qua O, vẽ đường thẳng vuông góc với \(O{A_2}\), trên đường thẳng này lấy điểm \({A_3}\) sao cho \(O{A_2}\; = {\rm{ }}O{A_3}\;\) và góc quay từ A 2 đến A 3 theo chiều kim đồng hồ. Khi đó A 3 là ảnh của điểm A 2 qua phép quay tâm O, góc quay – 90°. Tương tự, xác định được điểm B 3 là ảnh của điểm B 2 qua phép quay tâm O, góc quay – 90°. Vậy đoạn thẳng A 3 B 3 là ảnh của đoạn thẳng A 2 B 2 qua phép quay tâm O với góc quay \(\varphi = --90^\circ .\)

d) Vì phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì nên \(AB{\rm{ }} = {\rm{ }}{A_1}{B_1}.\)
Vì phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì nên \({A_1}{B_1}\; = {\rm{ }}{A_2}{B_2}.\)
Vì phép quay bảo toàn khoảng cách giữa hai điểm bất kì nên \({A_2}{B_2}\; = {\rm{ }}{A_3}{B_3}.\)Do đó, \(AB{\rm{ }} = {\rm{ }}{A_1}{B_1}\; = {\rm{ }}{A_2}{B_2}\; = {\rm{ }}{A_3}{B_3}.\)
Luyện tập 10
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm \(I\left( {--{\rm{ }}3;{\rm{ }}2} \right)\) bán kính \(R{\rm{ }} = {\rm{ }}1\). Thực hiện phép dời hình f bằng cách thực hiện liên tiếp phép đối xứng tâm O và phép tịnh tiến theo vectơ \(\vec u = \left( { - 1;\,3} \right)\). Xác định ảnh của đường tròn (C) qua phép dời hình nói trên.
Phương pháp giải:
Tìm ảnh của tâm I qua phép đối xứng tâm O và phép tịnh tiến theo vectơ \(\vec u = \left( { - 1;\,3} \right)\) bằng cách:
Nếu \(M'(x';y')\) là ảnh của \(M(x;y)\) qua phép tịnh tiến \({T_{\overrightarrow u }}\) , \(\overrightarrow u = \left( {a;\,b} \right)\) thì biểu thức tọa độ của phép tịnh tiến là \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)
Sau đó viết phương trình (C).
Lời giải chi tiết:
Ảnh của đường tròn (C) qua phép đối xứng tâm O là một đường tròn có bán kính bằng 1, gọi là (C').
Gọi I' là tâm của đường tròn (C'), khi đó I' là ảnh của I qua phép đối xứng tâm O. Suy ra I'(3; – 2). Do vậy, đường tròn (C') có tâm I'(3; – 2) và bán kính bằng 1.
Ảnh của đường tròn (C') qua phép tịnh tiến theo vectơ \(\vec u = \left( { - 1;\,3} \right)\) một đường tròn có bán kính bằng 1, gọi là (C").
Gọi I" là tâm của đường tròn (C"), khi đó I" là ảnh của I' qua phép tịnh tiến theo vectơ \(\vec u = \left( { - 1;\,3} \right)\) suy ra nên I"(2; 1). Do vậy, đường tròn (C") có tâm I"(2; 1) và bán kính bằng 1.
Vậy ảnh của đường tròn (C) qua phép dời hình f là đường tròn (C") có tâm I"(2; 1) và bán kính bằng 1.
Hoạt động 17
Quan sát Hình 37 .
a) Chỉ ra các phép dời hình biến tam giác ABC thành tam giác A 1 B 1 C 1 và biến tam giác \({A_1}{B_1}{C_1}\) thành tam giác \({A_2}{B_2}{C_2}.\)
b) Có nhận xét gì về hai tam giác ABC và \({A_2}{B_2}{C_2}?\)

Phương pháp giải:
Quan sát hình 37 và dựa vào kiến thức tịnh tiến, đối xứng trục để làm
Lời giải chi tiết:
) Quan sát Hình 37 , ta thấy phép tịnh tiến theo vectơ \(\vec u\) biến tam giác ABC thành tam giác A 1 B 1 C 1 và phép đối xứng trục d biến biến tam giác \({A_1}{B_1}{C_1}\) thành tam giác \({A_2}{B_2}{C_2}.\)
b) Theo tính chất của phép tịnh tiến và phép đối xứng trục, ta suy ra
\(AB{\rm{ }} = {\rm{ }}{A_1}{B_1}\; = {\rm{ }}{A_2}{B_2},{\rm{ }}BC{\rm{ }} = {\rm{ }}{B_1}{C_1}\; = {\rm{ }}{B_2}{C_2},{\rm{ }}AC{\rm{ }} = {\rm{ }}{A_1}{C_1}\; = {\rm{ }}{A_2}{C_2}.\)
Do đó, hai tam giác ABC và \({A_2}{B_2}{C_2}\) bằng nhau.
Luyện tập 11
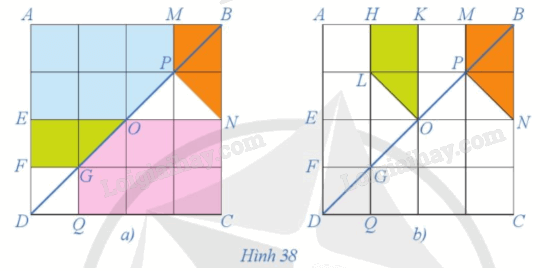
Quan sát Hình 38a và chứng minh hai hình AMPOE và CQGON bằng nhau.
Phương pháp giải:
Quan sát hình 38 và dựa vào kiến thức:
Cho điểm O, phép biến hình biến điểm O thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm M’ sao cho O là trung điểm của MM’ được gọi là phép đối xứn tâm O, kí hiệu \({Đ_O}\). Điểm O được gọi là tâm đối xứng.
Lời giải chi tiết:
Quan sát hình ta thấy \(OA{\rm{ }} = {\rm{ }}OC,{\rm{ }}OM{\rm{ }} = {\rm{ }}OQ,{\rm{ }}OP{\rm{ }} = {\rm{ }}OG,{\rm{ }}OE{\rm{ }} = {\rm{ }}ON\) nên O là trung điểm của các đoạn thẳng AC, MQ, PG, EN. Do đó, ta có phép đối xứng tâm O biến các điểm A, M, P, O, E tương ứng thành các điểm C, Q, G, O, N. Như vậy, phép đối xứng tâm O biến hình AMPOE thành hình CQGON. Vậy hai hình AMPOE và CQGON bằng nhau.