Giải mục III trang 94, 95 SGK Toán 7 tập 2 - Cánh diều — Không quảng cáo

III. Dấu hiệu nhận biết

HĐ 3

Cho tam giác ABC thỏa mãn $\widehat B = \widehat C$. Kẻ AH vuông góc với BC, H thuộc BC (Hình 74) .

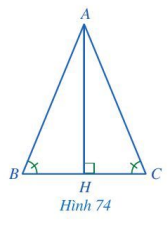
a) Hai tam giác BAH và CAH có bằng nhau hay không? Vì sao?

b) Hai cạnh AB và AC có bằng nhau hay không? Vì sao?

Phương pháp giải:

a) Xét hai tam giác BAH và CAH theo trường hợp g.c.g.

b) Sử dụng kết quả phần a) để xét hai cạnh AB và AC . Hai tam giác bằng nhau thì các cặp cạnh tương ứng bằng nhau

Lời giải chi tiết:

a) $\widehat B = \widehat C$. Mà tổng ba góc trong một tam giác bằng 180° nên $\widehat {BAH} = \widehat {CAH}$.

Xét hai tam giác BAH và CAH có:

$\widehat {BAH} = \widehat {CAH}$;

AH chung;

$\widehat {AHB} = \widehat {AHC}$ (= 90°).

Vậy $\Delta BAH = \Delta CAH$(g.c.g)

b) $\Delta BAH = \Delta CAH$ nên AB = AC ( 2 cạnh tương ứng).

LT - VD

Cho tam giác ABC cân tại A . Qua điểm M nằm giữa A và B kẻ đường thẳng song song với BC , cắt cạnh AC tại N . Chứng minh tam giác AMN cân.

Phương pháp giải:

Chứng minh tam giác AMN cân bằng cách chứng minh hai góc AMN và ANM bằng nhau.

Lời giải chi tiết:

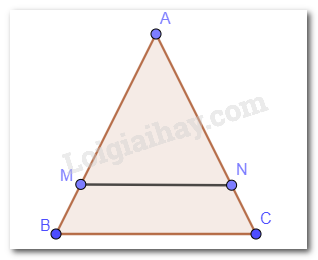
Ta có tam giác ABC cân mà MN // BC . Nên $\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}$ (đồng vị)

Mà $\widehat {ABC} = \widehat {ACB}$(tam giác ABC cân) nên $\widehat {AMN} = \widehat {ANM}$.

Vậy tam giác AMN cân tại A ( Tam giác có 2 góc bằng nhau)