Giải phần B. Kết nối trang 49 Bài tập phát triển năng lực Toán 4 tập 2
Tính a) 13 330 : (26 + 36) Đúng ghi Đ, sai ghi S: a) 29 900 = 299 x 100
Câu 6
Tính
a) 13 330 : (26 + 36)
b) 72 100 – 205 x 127
c) 55 x 22 + 7800 : 100
d) (216 x 7 - 87 x 9) : 9
Phương pháp giải:
- Nếu biểu thức có dấu ngoặc thì ta thực hiện các phép tính ở trong ngoặc trước. - Nếu biểu thức có các phép tính cộng, trừ, nhân, chia ta thực hiện các phép tính nhân, chia trước, thực hiện phép cộng, trừ sau
Lời giải chi tiết:
a) 13 330 : (26 + 36)
= 13 330 : 62
= 215
b) 72 100 – 205 x 127
= 72 100 – 26 035
= 46 065
c) 55 x 22 + 7800 : 100
= 1210 + 78
= 1288
d) (216 x 7 - 87 x 9) : 9
= (1512 – 783) : 9
= 729 : 9 = 81
Câu 7
Đúng ghi Đ, sai ghi S:
a) 29 900 = 299 x 100
b) 65 700 > 657 x 1000
c) 40 800 : 100 = 408
d) 33 x 77 < 37 x 73
Phương pháp giải:
Thực hiện lại các phép tính để kiểm tra kết quả của từng câu.
Lời giải chi tiết:
a) 29 900 = 299 x 100 Đ
b) 65 700 > 657 x 1000 S
c) 40 800 : 100 = 408 Đ
d) 33 x 77 < 37 x 73. Đ
Câu 8
Biểu đồ bên dưới cho biết số lượng xe máy của bốn phường A, B, C, D:
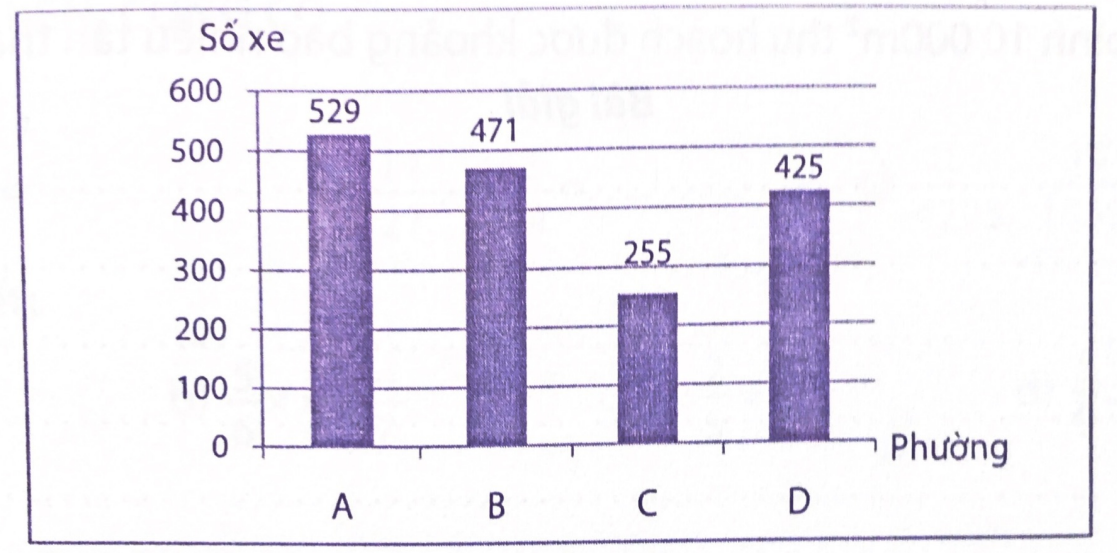
Nhìn biểu đồ, viết số thích hợp vào chỗ trống:
a) Số lượng xe máy ở phường A là:. . . . . . . xe máy.
b) Số lượng xe máy ở phường B là:. . . . . . . xe máy.
c) Số lượng xe máy ở phường C là:. . . . . . . xe máy.
d) Số lượng xe máy ở phường D là:. . . . . . . xe máy.
e) Tổng số xe máy của 4 phường là:. . . . . . . xe máy.
Phương pháp giải:
Quan sát biểu đồ để trả lời câu hỏi của đề bài.
Lời giải chi tiết:
a) Số lượng xe máy ở phường A là: 529 xe máy.
b) Số lượng xe máy ở phường B là: 471 xe máy.
c) Số lượng xe máy ở phường C là: 255 xe máy.
d) Số lượng xe máy ở phường D là: 425 xe máy.
e) Tổng số xe máy của 4 phường là: 529 + 471 + 255 + 425 = 1680 xe máy.
Câu 9
Tìm 4 phân số lớn hơn phân số $\frac{{10}}{{11}}$ và bé hơn phân số $\frac{{11}}{{12}}$ .
Phương pháp giải:
- Quy đồng mẫu số hai phân số.
- Xác định 4 phân số lớn hơn $\frac{{10}}{{11}}$ và bé hơn $\frac{{11}}{{12}}$
Lời giải chi tiết:
Ta có: $\frac{{10}}{{11}} = \frac{{600}}{{660}}\,\,\,\,\,;\,\,\,\,\frac{{11}}{{12}} = \frac{{605}}{{660}}$.
Vậy 4 phân số lớn hơn phân số $\frac{{10}}{{11}}$ và bé hơn phân số $\frac{{11}}{{12}}$là: $\frac{{601}}{{660}};\frac{{602}}{{660}};\frac{{603}}{{660}};\frac{{604}}{{660}}$hay $\frac{{601}}{{660}};\frac{{301}}{{330}};\frac{{201}}{{220}};\frac{{151}}{{165}}$