Bài 7. Phương trình trạng thái của khí lí tưởng trang 26, 27, 28 SBT Vật lí 12 Chân trời sáng tạo
Biểu thức nào sau đây không đúng khi xét quá trình biến đổi đẳng tích của một khối lượng khí lí tưởng xác định?
Trắc nghiệm 7.1
Biểu thức nào sau đây không đúng khi xét quá trình biến đổi đẳng tích của một khối lượng khí lí tưởng xác định?
A. \(\frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}}\)
B. \(\frac{{{p_1}}}{{{p_2}}} = \frac{{{T_1}}}{{{T_2}}}\)
C. \({p_1}{T_2} = {p_2}{T_1}\)
D. \(\frac{{{p_1}}}{{{p_2}}} = \frac{{{T_2}}}{{{T_1}}}\)
Phương pháp giải:
Vận dụng kiến thức về quá trình biến đổi đẳng tích
Lời giải chi tiết:
Quá trình biến đổi đẳng tích: \(\frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}}\)
Nên \(\frac{{{p_1}}}{{{p_2}}} = \frac{{{T_2}}}{{{T_1}}}\) không đúng
Đáp án: D
Trắc nghiệm 7.2
Một khối khí lí tưởng thực hiện quá trình biến đổi đẳng tích ở hai thể tích khác nhau được biểu diễn như Hình 7.1. Quan hệ giữa V 1 và V 2 là:
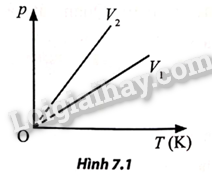
A. \[{V_1} > {V_2}\]
B. \[{V_1} < {V_2}\]
C. \[{V_1} = {V_2}\]
D. không so sánh được.
Phương pháp giải:
Vận dụng kiến thức về quá trình biến đổi đẳng tích
Lời giải chi tiết:
Có: \({p_1} < {p_2}\)và \({T_1} > {T_2}\) nên \(\frac{{{p_1}}}{{{T_1}}} > \frac{{{p_2}}}{{{T_2}}} \Rightarrow {V_1} > {V_2}\)
Đáp án: A
Trắc nghiệm 7.3
Quá trình nào sau đây không phải là quá trình đẳng tích?
A. Bọt khí nổi lên và to dần từ đáy một hồ nước.
B. Bánh xe đạp bị mềm hơn do nhiệt độ giảm.
C. Quả bóng cao su được phơi ngoài nắng.
D. Khối khí chứa trong xilanh có pit-tông cố định.
Phương pháp giải:
Vận dụng kiến thức về quá trình đẳng tích
Lời giải chi tiết:
Vì trong quá trình nổi lên từ đáy hồ, bọt khí tăng dần kích thước do đây là quá trình đẳng nhiệt.
Đáp án: A
Trắc nghiệm 7.4
Một chiếc lốp ô tô chứa không khí ở áp suất 5 atm, nhiệt độ 27 °C. Khi xe chạy, nhiệt độ của khí trong lốp tăng lên đến 54 °C, coi thể tích lốp xe không thay đổi, áp suất không khí trong lốp khi đó là
A. 10 atm.
B. 5,45 atm.
C. 4,55 atm.
D. 10,45 atm.
Phương pháp giải:
Vận dụng kiến thức về quá trình đẳng tích
Lời giải chi tiết:
Ta có: \({p_2} = \frac{{{T_2}}}{{{T_1}}}.{p_1} = \frac{{54 + 273}}{{27 + 273}}.5 = 5,45(atm)\)
Đáp án: B
Trắc nghiệm 7.5
Một bình kín có thể tích 12 lít, chứa nitrogen ở áp suất 80 atm có nhiệt độ 17 °C, xem nitrogen là khí lí tưởng. Khối lượng nitrogen trong bình xấp xỉ giá trị nào sau đây? Biết khối lượng mol của nitrogen là 28 g/mol.
A. 1,13 kg.
B. 1,13 g.
C. 0,113 g.
D. 0,113 kg.
Phương pháp giải:
Vận dụng kiến thức về quá trình đẳng tích
Lời giải chi tiết:
Ta có: \(m = \frac{{pV}}{{RT}}.M = \frac{{{{80.1,01.10}^5}.0,012}}{{8,31.290}}.28 \approx 1126,55(g) \approx 1,13kg\)
Đáp án: A
Trắc nghiệm 7.6
Hai phòng kín có thể tích bằng nhau, thông với nhau bằng một cửa mở. Nhiệt độ không khí trong hai phòng khác nhau, số phân tử khí trong mỗi phòng như thế nào?
A. Bằng nhau.
B. Phòng nóng chứa nhiều phân tử hơn.
C. Phòng lạnh chứa nhiều phân tử hơn.
D. Tuỳ theo kích thước của cửa.
Phương pháp giải:
Vận dụng kiến thức về quá trình đẳng tích
Lời giải chi tiết:
Áp suất khí tăng khi nhiệt độ tăng và mật độ phân tử khí tăng.
Khi hai phòng mở cửa thì áp suất khí bằng nhau. Do phòng nóng có nhiệt độ cao hơn nên áp suất có xu hướng tăng lên so với phòng lạnh. Để áp suất hai phòng bằng nhau thì mật độ phân tử khí ở phòng nóng phải thấp hơn so với phòng lạnh. Do thể tích hai phòng như nhau, nên số phân tử khí trong phòng nóng sẽ ít hơn so với phòng lạnh (mật độ phân tử khí \(\mu = \frac{N}{V}\))
Đáp án: C
Trắc nghiệm 7.7
Khối khí trong xilanh của một động cơ nhiệt có áp suất là 0,8.10 5 Pa và nhiệt độ là 50 °C. Sau khi bị nén, thể tích của khí giảm 5 lần còn áp suất tăng lên đến 7.10 5 Pa. Nhiệt độ của khí ở cuối quá trình nén xấp xỉ giá trị nào sau đây?
A. 292 °C.
B. 565 °C.
C. 292 K.
D. 87,5 °C.
Phương pháp giải:
Vận dụng kiến thức về khí lí tưởng
Lời giải chi tiết:
Ta có: \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}} \Rightarrow {T_2} = \frac{{{p_2}{V_2}}}{{{p_1}{V_1}}}.{T_1} = \frac{{{{7.10}^5}.\frac{{{V_1}}}{5}}}{{{{0,8.10}^5}.{V_1}}}.(50 + 273) = 565,25(K) = 292,25{(^o}C)\)
Đáp án: A
Trắc nghiệm 7.8
Một bình kín chứa 1 mol nitrogen, áp suất khí là 103 Pa, ở nhiệt độ 27 °C. Trong mỗi phát biểu sau, em hãy chọn đúng hoặc sai.
a) Thể tích của bình xấp xỉ bằng 25 lít.
b) Nung bình đến khi áp suất khí bằng 5.10 5 Pa. Nhiệt độ của khối khí khi đó
là 135 °C.
c) Giả sử một lượng khí thoát ra ngoài nên áp suất khí trong bình giảm còn 4.10 5 Pa, nhiệt độ vẫn được giữ không đổi so với câu b. Lượng khí đã thoát ra ngoài là 0,2 mol.
Phương pháp giải:
Vận dụng kiến thức về khí lí tưởng
Lời giải chi tiết:
a) Đúng: \(V = \frac{{nRT}}{p} = \frac{{1.8,31.(27 + 273)}}{{{{10}^5}}} \approx 0,025({m^3}) = 25(l)\)
b) Sai: \({T_2} = \frac{{{p_2}}}{{{p_1}}}.{T_1} = \frac{{{{5.10}^5}}}{{{{10}^5}}}.(27 + 273) = 1500(K) = 1227{(^o}C)\)
c) Đúng:
Áp dụng phương trình trạng thái:
\(\frac{{{p_1}V}}{{{n_1}{T_1}}} = \frac{{{p_3}V}}{{{n_3}{T_3}}} \Rightarrow {n_3} = \frac{{{n_1}{T_1}{p_3}}}{{{T_3}{p_1}}} = \frac{{1.(27 + 273){{.4.10}^5}}}{{{{1500.10}^5}}} = 0,8(mol)\)
Suy ra: Lượng khí thoát ra là 0,2 mol.
Trắc nghiệm 7.9
Một bình bằng thép có dung tích 50 lít chứa helium ở áp suất 5 MPa và nhiệt độ là 37 °C. Dùng bình này bơm được bao nhiêu quả bóng bay? Biết dung tích mỗi quả là 10 lít, áp suất mỗi quả là 1,05.10 5 Pa, nhiệt độ khí trong bóng bay là 12 °C.
A. 200 quả.
B. 250 quả.
C. 237 quả.
D. 214 quȧ.
Phương pháp giải:
Vận dụng kiến thức về khí lí tưởng
Lời giải chi tiết:
Gọi N là số quả bóng bơm được. Áp dụng công thức:
\(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}(n{V_2} + {V_1})}}{{{T_2}}} \Rightarrow \frac{{{{5.10}^6}.50}}{{37 + 273}} = \frac{{{{1,05.10}^5}.(10n + 50)}}{{12 + 273}} \Rightarrow n \approx 214\) quả
Đáp án: D
Trắc nghiệm 7.10
Xét một động cơ xăng 4 kì của ô tô. Trong quá trình pit-tông nén hỗn hợp khí (gọi là kì nén), nhiệt độ khí tăng từ 43 °C đến 300 °C, thể tích của khí giảm từ 1,8 lít đến 0,2 lít. Áp suất của khí lúc bắt đầu nén là 90 kPa. Coi hỗn hợp khí như chất khí thuần nhất và tuân theo các định luật chất khí, áp suất hỗn hợp khí ở cuối kì nén là
A. 0,45.10 6 Pa.
B. 1,47.10 6 Pa.
C. 1,81.10 4 Pa.
D. 2,4.10 6 Pa.
Phương pháp giải:
Vận dụng kiến thức về khí lí tưởng
Lời giải chi tiết:
Ta có: \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}} \Rightarrow {p_2} = \frac{{{p_1}{V_1}.{T_2}}}{{{V_2}{T_1}}} = \frac{{{{90.10}^3}.1,8.(300 + 273)}}{{0,2.(43 + 273)}} \approx {1,47.10^6}(Pa)\)
Đáp án: B
Tự luận 7.1
Viết phương trình trạng thái của khí lí tưởng và giải thích các đại lượng trong phương trình.
Phương pháp giải:
Vận dụng kiến thức về khí lí tưởng
Lời giải chi tiết:
Phương trình trạng thái của khí lí tưởng: \(\frac{{pV}}{T} = nR\)
Xét khối khí lí tưởng xác định
p là áp suất khí (Pa)
V là thể tích của khối khí (m 3 )
T là nhiệt độ tuyệt đối của khí (K)
n là số mol khí (mol)
R ≈ 8,31 \(\frac{J}{{mol.K}}\) là hằng số khí lí tưởng
Tự luận 7.2
Xét một khối khí lí tưởng xác định. Đồ thị trong Hình 7.2 mô tả đẳng quá trình nào? Giải thích.

Phương pháp giải:
Vận dụng kiến thức về khí lí tưởng
Lời giải chi tiết:
Quá trình đẳng tích vì đồ thị trong hệ toạ độ \[pOT\]có dạng đường thẳng và có đường kéo dài qua gốc toạ độ O.
Tự luận 7.3
Một khối khí lí tưởng ở nhiệt độ 47 °C được nung nóng đến khi áp suất tăng lên 3 lần và thể tích giảm 2 lần. Xác định nhiệt độ của khối khí sau khi nung.
Phương pháp giải:
Vận dụng kiến thức về khí lí tưởng
Lời giải chi tiết:
Áp dụng phương trình trạng thái của khí lí tưởng:
\(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}} \Rightarrow {T_2} = \frac{{{p_2}{V_2}}}{{{p_1}{V_1}}}.{T_1} = \frac{{3{p_1}.\frac{{{V_1}}}{2}}}{{{p_1}.{V_1}}}.(47 + 273) = 480(K) = 207{(^o}C)\)
Tự luận 7.4
Một săm xe máy được bơm căng không khí ở nhiệt độ 22 °C và áp suất 2 atm. Nếu để xe ngoài trời nắng và nhiệt độ của khí trong săm xe tăng đến 50 °C thì săm xe có bị nổ không? Coi sự tăng thể tích của săm xe là không đáng kể và săm xe chỉ chịu được áp suất tối đa là 2,5 atm.
Phương pháp giải:
Vận dụng kiến thức về quá trình đẳng tích
Lời giải chi tiết:
Ta có: \({p_2} = \frac{{{T_2}}}{{{T_1}}}.{p_1} = \frac{{323}}{{295}}.2 \approx 2,19(atm) < 2,5atm\) nên săm xe không bị nổ.
Tự luận 7.5
Bóng đèn sợi đốt (bóng đèn dây tóc) còn được gọi tắt là bóng đèn tròn (Hình 7.3), là loại bóng đèn trước đây được sử dụng rộng rãi trong cuộc sống. Trong lĩnh vực nông nghiệp, đèn sợi đốt được người dân sử dụng để kích thích cây ra hoa trái vụ, thu hoạch được sản lượng cao hơn. Tuy nhiên, hiệu suất phát sáng của loại đèn này thấp, điện năng tiêu thụ nhiều, gây lãng phí nên ngày nay đèn này đã được thay thế bởi các loại đèn tiết kiệm năng lượng hơn như đèn LED, Compact,... Bộ phận chính của đèn sợi đốt gồm: sợi đốt làm bằng wolfram, chịu được nhiệt độ cao; bóng thuỷ tinh làm bằng thuỷ tinh chịu nhiệt, bên trong được bơm khí trơ ở áp suất thấp.

a) Trình bày nguyên tắc phát sáng của đèn. Tại sao đèn sợi đốt lại có hiệu suất chiếu sáng thấp?
b) Vì sao sợi đốt làm bằng kim loại wolfram?
c) Vì sao trong bóng thuỷ tinh cần phải bơm đầy khí trơ ở áp suất thấp?
d) Bóng đèn sợi đốt có lớp vỏ làm bằng thuỷ tinh chịu nhiệt nên nhiệt độ khi đèn sáng có thể đạt tới 260 °C, coi áp suất khí trong bóng đèn bằng với áp suất khí quyển là 1 atm. Tính áp suất khí trong bóng đèn khi đèn chưa sáng ở nhiệt độ 25°C.
Phương pháp giải:
Vận dụng kiến thức về khí lí tưởng
Lời giải chi tiết:
a) Khi có dòng điện chạy qua đèn, sợi đốt của đèn toả nhiệt và nóng dần đến phát sáng. Khi đó điện năng được chuyển hoá thành nhiệt năng, sau đó một phần nhỏ nhiệt năng được chuyển hoá thành quang năng. Do đó hiệu suất chiếu sáng
của đèn sợi đốt thấp so với các loại đèn khác.
b) Để đèn phát sáng thì sợi đốt phải có nhiệt độ rất cao và không bị nóng chảy. Wolfram là kim loại có nhiệt độ nóng chảy cao nhất nên được lựa chọn để làm
sợi đốt bóng đèn.
c) Coi thuỷ tinh dãn nở không đáng kể, thể tích khí trong bóng đèn coi như không đổi. Khi đèn sáng nhiệt độ của sợi đốt tăng cao làm nhiệt độ khí trong bóng đèn tăng lên kéo theo áp suất khi tăng (do áp suất tỉ lệ với nhiệt độ tuyệt đối) có thể gây nổ đèn nếu là khí thường ở áp suất thường. Sử dụng khí trơ ở áp suất thấp vừa làm giảm sự oxi hoá của sợi đốt (do không gây ra phản ứng hóa học), vừa làm chậm sự tăng của áp suất khí trong bình, hạn chế nguy cơ nổ đèn.
d) Vì thể tích khí trong bóng đèn không thay đổi.
Ta có: \({p_1} = \frac{{{T_1}}}{{{T_2}}}.{p_2} = \frac{{298}}{{533}} \approx 0,56(atm)\)
Tự luận 7.6
Một bình chứa oxygen sử dụng trong y tế có thể tích 14 lít, áp suất 15.10 6 Pa và nhiệt độ phòng 27 °C.
a) Tính khối lượng oxygen trong bình. Biết khối lượng mol của oxygen là 32 g/mol.
b) Theo thông tin từ bộ y tế, thông thường đối với một bệnh nhân mắc bệnh COVID 19 được chỉ định dùng liệu pháp oxy, thì người bệnh cần được cung cấp trung bình 6 lít oxygen trong 15 phút. Hãy cho biết với tốc độ thở như vậy thì bao lâu người đó dùng hết bình oxygen 14 lít.
Phương pháp giải:
Vận dụng kiến thức về khí lí tưởng
Lời giải chi tiết:
a) Áp dụng phương trình trạng thái khí lí tưởng:
\(pV = nRT \to n = \frac{{pV}}{{RT}} = \frac{{{{15.10}^6}.0,014}}{{8,31.300}} \approx 84,24(mol)\)
Khối lượng oxygen trong bình là: \(m = nM = 84,24.32 = 2696(g) = 2,696(kg)\)
b) Oxygen đi vào với lưu lượng 6 lít/15 phút \( \Leftrightarrow \) 0,4 lít/phút.
Ta có: \[V' = 22,4n'\].
Số mol khí người đó hít trong 1 phút là:\(n' = \frac{{V'}}{{22,4}} = \frac{{0,4}}{{22,4}} \approx 0,018(mol)\)
Số gam khí người đó hít trong 1 phút là: \(m' = n'.32 = 0,018.32 = 0,576(g)\)
Thời gian người đó dùng hết bình oxygen là: \(t = \frac{m}{{m'}} = \frac{{2696}}{{0,576}} \approx 4681\) (phút)\( \approx 78\)giờ
Tự luận 7.7
Bóng thám không (Hình 7.4) là một thiết bị được sử dụng phổ biến trong ngành khí tượng để thu thập dữ liệu về các thông số thời tiết như nhiệt độ, độ ẩm, áp suất và hướng gió ở độ cao khác nhau của bầu khí quyển. Trên quả bóng có gắn thiết bị gọi là Radiosonde có chức năng ghi nhận các dữ liệu thông qua các cảm biến và phát tín hiệu radio để truyền dữ liệu trở lại mặt đất để các nhà khoa học và nhà khí tượng có thể thu thập và phân tích. Bóng thám không thường được làm từ cao su hoặc các vật liệu nhẹ có khả năng chịu biến dạng. Bóng được bơm khí nhẹ như hydrogen hoặc helium.

a) Tại sao lại phải bơm khí nhẹ vào bóng?
b) Bóng thám không có thể bay lên cao mãi được không? Giải thích.
c) Mặc dù phải thả các bóng thám không hàng ngày, chi phí mua mỗi quả bóng là khá đáng kể và việc tái sử dụng Radiosonde khi rơi xuống sẽ tiết kiệm được kinh phí, góp phần bảo vệ môi trường nhưng đa số các trạm quan sát khí tượng đều dùng bóng thám không sử dụng một lần mà không tái sử dụng. Hãy giải thích lí do.
d) Hãy đề xuất phương án để thiết bị Radiosonde khi rơi xuống có thể tái sử dụng. e) Giả sử một quả bóng thám không kín có thể tích ban đầu là 20 m chứa hydrogen và có tổng khối lượng (khối lượng quả bóng và thiết bị đo) là 6 kg. Tính độ cao của quả bóng cho đến khi bị nổ. Biết rằng khi thể tích quả bóng tăng gấp 27 lần thể tích ban đầu thì quả bóng bị nổ; áp suất khí quyển giảm theo độ cao với quy luật \({p_k} = {p_o}{e^{ - \frac{{{M_k}gh}}{{RT}}}}\); nhiệt độ ở độ cao mà bóng bị nổ là 218 K. Áp suất khí quyển ở mặt đất là 10 5 Pa; khối lượng mol của phân tử không khí và hydrogen lần lượt là 29 g/mol và 2 g/mol; gia tốc trọng trường là 9,8 m/s.
Phương pháp giải:
Vận dụng kiến thức về khí lí tưởng
Lời giải chi tiết:
a) Khi bơm loại khí nhẹ hơn không khí, lực đẩy Archimedes tác dụng lên quả bóng lớn hơn trọng lực tác dụng lên nó, làm bóng thám không có thể bay lên cao.
b) Càng lên cao, không khí càng loãng, áp suất khí quyển giảm dần, tạo ra sự chênh lệch áp suất bên trong và ngoài bóng, quả bóng phình to dần (thể tích tăng), bề mặt cao su của quả bóng bị dãn ra. Khi vượt quá giới hạn đàn hồi của vật liệu làm vỏ bóng thì bóng bị vỡ. Như vậy, bóng thám không không thể bay lên cao mãi, nó sẽ đạt đến độ cao nhất định và bị vỡ/nổ trong không khí.
c) Đa số hiện nay các bóng thám không được sử dụng để theo dõi thời tiết đều là bóng sử dụng một lần mà không tái sử dụng dựa trên các yếu tố kinh tế, kĩ thuật và thực tiễn.
– Tính kĩ thuật và thực tiễn: Thiết bị khi rơi xuống có thể bị trục trặc, hư hỏng; việc thu hồi bóng thám không có thể rất khó khăn nếu chúng rơi ở những vùng xa xôi, khó tiếp cận hoặc trong điều kiện thời tiết khắc nghiệt.
– Tính kinh tế: Giá thành một quả bóng thám không cũng không quá lớn và thấp hơn so với chi phí thu hồi thiết bị của bóng và chỉnh sửa, căn chỉnh thiết bị khi tái sử dụng.
d) Đề xuất phương án để thiết bị Radiosonde khi rơi xuống có thể tái sử dụng:
– Gắn thêm dù hạ cánh để hạn chế tốc độ rơi của Radiosonde khi rơi trong không khí.
– Lắp đặt bộ giảm xóc hoặc vật liệu hấp thụ xung lực xung quanh Radiosonde để giảm thiểu ảnh hưởng của va đập khi tiếp đất.
e) Bỏ qua áp suất phụ do vật liệu làm vỏ quả bóng gây ra, nên áp suất khí bên trong quả bóng và áp suất khí quyển bên ngoài là bằng nhau,\[p = {p_o}\]
Khi quả bóng bay lên đến độ cao cực đại h (ngay trước khi bị nổ), nó ở trạng thái cân bằng, trọng lực tác dụng lên quả bóng cân bằng với lực đẩy Archimedes.
Hay: \[{m_b}g = {\rho _k}{V_h}g \Rightarrow {m_b} = {\rho _k}{V_h}\] (1) (\({m_b}\)là tổng khối lượng của quả bóng và thiết bị).
Trong đó: \({V_h}\) là thể tích quả bóng ở độ cao h.
\({\rho _k}\)là khối lượng riêng của không khí ở độ cao h .
Từ phương trình trạng thái: \({p_k}{V_h} = \frac{{{m_k}}}{{{M_k}}}RT \Rightarrow {\rho _k} = \frac{{{p_k}{M_k}}}{{RT}}\)
Thay vào (1) ta có: \({m_b} = \frac{{{p_o}{e^{ - \frac{{{M_k}gh}}{{RT}}}}.{M_k}.{V_h}}}{{RT}}\)
Thay số: p o = 10 5 Pa, T = 218 K, M k = 29 g/mol, g = 9,8 m/s 2 , R = 8,31 \(\frac{J}{{mol.K}}\), V h = 27.20 = 540 m 3 , m b = 6 kg.
Suy ra: \(h = 31682m = 31,683km\)
Như vậy, quả bóng bay lên đến độ cao 31,682 km thì bị nổ.