Bài 3. Vận tốc, gia tốc trong dao động điều hòa trang 8, 9 SBT Vật lí 11 Kết nối tri thức với cuộc sống
Chọn kết luận đúng về dao động điều hoà.
3.1
Chọn kết luận đúng về dao động điều hoà.
A. Quỹ đạo là đường hình sin. B. Quỹ đạo là một đoạn thẳng.
C. Vận tốc tỉ lệ thuận với thời gian. D. Gia tốc tỉ lệ thuận với thời gian
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với:
+ \(x\) là li độ dao động.
+ \(A\) là biên độ dao động.
+ \(\omega \) là tần số góc của dao động.
+ \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t.
+\(\varphi \) là pha ban đầu.
Lời giải chi tiết:
Quỹ đạo của dao động điều hòa có thể là một hình sin
Đáp án A
3.2
Tìm phát biểu sai khi nói về dao động điều hoà.
A. Gia tốc sớm pha \(\pi \) với li độ.
B. Li độ và gia tốc luôn ngược pha nhau.
C. Vận tốc luôn trễ pha \(\frac{\pi }{2}\) so với gia tốc.
D. Vận tốc luôn trễ pha \(\frac{\pi }{2}\) so với li độ.
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Phương trình của vận tốc có dạng : \(v = A\omega \cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\)
Phương trình của gia tốc có dạng : \(a = A{\omega ^2}\cos \left( {\omega t + \varphi + \pi } \right)\)
Lời giải chi tiết:
Từ phương trình vận tốc và li độ ta có : Li độ luôn trễ pha \(\frac{\pi }{2}\) so với vận tốc
Đáp án :D
3.3
Vận tốc của một vật dao động điều hoà khi đi qua vị trí cân bằng là 1 cm/s và gia tốc của vật khi ở vị trí biên là 1,57\(cm/{s^2}\). Chu kì dao động của vật là
A. 3,24 s. B. 6,28 s. C. 4 s. D. 2 s.
Phương pháp giải:
Phương trình của vận tốc có dạng : \(v = A\omega \cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\)
- Khi vật ở VTCB : \(v = \pm \omega A\)
- Khi vật ở vị trí biên : \(v = 0\)
Phương trình của gia tốc có dạng : \(a = A{\omega ^2}\cos \left( {\omega t + \varphi + \pi } \right)\)
- Khi vật ở VTCB : \(a = 0\)
- Khi vật ở vị trí biên : \(a = \pm {\omega ^2}A\)
Lời giải chi tiết:
Khi vật ở VTCB ta có : \(v = A\omega = 1\) (1)
Khi vật ở vị trí biên ta có : \(a = A{\omega ^2} = 1,57\) (2)
Từ (1) và (2) => \(\frac{a}{v} = \frac{{A{\omega ^2}}}{{A\omega }} = \omega = \frac{{1,57}}{1} = 1,57(rad/s)\)
=> \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{1,57}} = 4\left( s \right)\)
Đáp án : C
3.4
Một chất điểm dao động điều hoà với tần số 4 Hz và biên độ dao động 10 cm. Độ lớn gia tốc cực đại của chất điểm bằng
A. 2,5 \(cm/{s^2}\) B. 25 \(cm/{s^2}\) C. 63,1 \(cm/{s^2}\) D. 6,31 \(cm/{s^2}\)
Phương pháp giải:
Phương trình của gia tốc có dạng : \(a = A{\omega ^2}\cos \left( {\omega t + \varphi + \pi } \right)\)
- Khi vật ở VTCB : \(a = 0\)
- Khi vật ở vị trí biên : \(a = \pm {\omega ^2}A\)
Lời giải chi tiết:
Đổi : 10 cm = 0,1 m
Ta có tần số của dao động : \(\)\(f = 4Hz = > \omega = 2\pi f = 2\pi .4 = 8\pi (rad/s)\)
Độ lớn gia tốc cực đại của chất điểm bằng: \(a = {\omega ^2}A = {(8\pi )^2}.0,1 = 63,1(m/{s^2})\)
Đáp án : C
3.5
Một chất điểm chuyền động tròn đều trên một đường tròn với tốc độ dài 160 cm/s và tốc độ góc 4 rad/s. Hình chiều P của chát điểm M trên một đường thẳng có định nằm trong mặt phăng hình tròn dao động điều hoà với biên độ và chu kì lần lượt là
A. 40 cm ; 0,25 s. B. 40 cm ; 1,57 s.
C. 40 m ; 0,25 s. D. 25 m ; 0,25 s.
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng đặc trưng của dao động điều hoà.
Tần số góc \(\omega = \frac{{2\pi }}{T} = 2\pi f(rad/s)\)
Phương trình của vận tốc có dạng : \(v = A\omega \cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\)
- Khi vật ở VTCB : \(v = \pm \omega A\)
- Khi vật ở vị trí biên : \(v = 0\)
Lời giải chi tiết:
Ta có: \(v = \omega R = \omega A = 160 = > A = \frac{v}{\omega } = 40(cm)\)
Chu kì dao động : \(T = \frac{{2\pi }}{\omega } = 1,57(s)\)
Đáp án : B
3.6
Phương trình vận tốc của một vật dao động của một vật là: \(v = 120\cos 20t\left( {cm/s} \right)\), với t đo bằng giây. Vào thời điểm \(t = \frac{T}{6}\) (T là chu kì dao động), vật có li độ là
A.3 cm. B. \( - 3\) cm. C. \(3\sqrt 3 \) cm. D. \( - 3\sqrt 3 \) cm.
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Phương trình của vận tốc có dạng : \(v = A\omega \cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\)
Lời giải chi tiết:
Từ phương trình của vận tốc => phương trình li độ của dao động :\(x = 6\cos (20t - \frac{\pi }{2})(cm)\)
Chu kì dao động của vật : \(T = \frac{{2\pi }}{\omega } = 0,2\pi (s)\)
=> Thời điểm \(t = \frac{T}{6} = \frac{{0,2\pi }}{6} = \frac{\pi }{{30}}(s)\)
Thay \(t = \frac{\pi }{{30}}\) vào phương trình li độ ta được : \(x = 6\cos (20.\frac{\pi }{{30}} - \frac{\pi }{2}) = 3\sqrt 3 (cm)\)
Đáp án : C
3.7
Một chất điểm dao động điều hoà. Biết li độ và vận tốc của chất điểm tại thời điểm \({t_1}\), lần lượt là \({x_1} = 3cm\) và \({v_1} = - 60\sqrt 3 \)cm/s; tại thời điểm \({t_2}\) ; lần lượt là \({x_2} = 3\sqrt 2 cm\) và \({v_2} = 60\sqrt 2 \)cm/s. Biên độ và tần số góc của dao động lần lượt bằng
A. 6cm ; 20 rad/s. B. 6 cm ; 12 rad/s.
C. 12 cm ; 20 rad/s. D. 12 cm ; 10 rad/s.
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Phương trình của vận tốc có dạng : \(v = A\omega \cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\)
Công thức độc lập với thời gian :
\({\left( {\frac{x}{A}} \right)^2} + {\left( {\frac{v}{{A\omega }}} \right)^2} = 1\)
Lời giải chi tiết:
Tại thời điểm \({t_1}\) : \({\left( {\frac{{{x_1}}}{A}} \right)^2} + {\left( {\frac{{{v_1}}}{{A\omega }}} \right)^2} = 1 = > {\left( {\frac{3}{A}} \right)^2} + \left( {\frac{{ - 60\sqrt 3 }}{{A\omega }}} \right) = 1\)
Tại thời điểm \({t_2}\) : \({\left( {\frac{{{x_2}}}{A}} \right)^2} + {\left( {\frac{{{v_2}}}{{A\omega }}} \right)^2} = 1 = > {\left( {\frac{{3\sqrt 2 }}{A}} \right)^2} + \left( {\frac{{60\sqrt 2 }}{{A\omega }}} \right) = 1\)
Giải hệ phương trình trên ta được :
\({A^2} = 36 = > A = 6(cm)\)
\({\left( {A\omega } \right)^2} = 14400 = > \omega = 20(rad/s)\)
Đáp án : A
3.8
Một dao động điều hoà trên đoạn thẳng dài 10 cm và thực hiện được 50 dao động trong thời gian 78,5 s. Tìm vận tốc và gia tốc của vật khi đi qua vị trí có li độ x = \( - 3\) cm theo chiều hướng về vị trí cân bằng.
Phương pháp giải:
Công thức độc lập với thời gian :
\({\left( {\frac{x}{A}} \right)^2} + {\left( {\frac{v}{{A\omega }}} \right)^2} = 1\)
Chiều đai quỹ đạo L= 2A
Lời giải chi tiết:
Biên độ của con lắc là : \(A = \frac{L}{2} = 5(cm)\)
Chu kì của con lắc : \(T = \frac{t}{n} = \frac{{78,5}}{{50}} = 1,57(s)\)
Tần số góc của con lắc : \(\omega = \frac{{2\pi }}{T} = 4(rad/s)\)
Ta có công thức độc lập với thời gian :
\({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2} = > {\left( { - 3} \right)^2} + \frac{{{v^2}}}{{{4^2}}} = {5^2} = > v = 16(cm/s)\)
3.9
Một vật dao động điều hoà với tằn số góc \(\omega \) = 5 rad/s. Khi t = 0, vật đi qua vị trí có li độ x = \( - 2\) cm và có vận tốc 10 cm/s hướng về vị trí biên gần nhất. Hãy viết phương trình dao động của vật.
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Công thức độc lập với thời gian :
\({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}\)
Lời giải chi tiết:
Thay x = \( - 2\) và v = 10 vào công thức độc lập với thời gian ta được :
\({A^{^2}} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {\left( { - 2} \right)^2} + \frac{{{{10}^2}}}{{{5^2}}} = > A = 2\sqrt 2 \)
Tại t = 0 ,ta có \(x = - 2 = 2\sqrt 2 \cos \left( \varphi \right) = > \cos \left( \varphi \right) = \frac{{ - \sqrt 2 }}{2}\) và v < 0
\( = > \varphi = \frac{{3\pi }}{4}\) => Phương trình dao động của vật là : \(x = 2\sqrt 2 \cos \left( {5t + \frac{{3\pi }}{4}} \right)cm\)
3.10
Hình 3.1 mô tả sự biến thiên vận tốc theo thời gian của một vật dao động điều hoà.
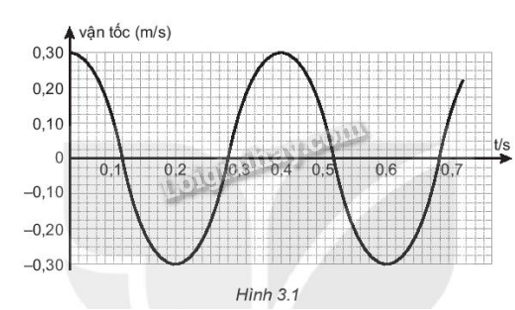
a) Viết phương trình vận tốc theo thời gian.
b) Viết phương trình li độ và gia tốc theo thời gian.
Phương pháp giải:
Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Phương trình của vận tốc có dạng : \(v = A\omega \cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\)
- Khi vật ở VTCB : \(v = \pm \omega A\)
- Khi vật ở vị trí biên : \(v = 0\)
Phương trình của gia tốc có dạng : \(a = A{\omega ^2}\cos \left( {\omega t + \varphi + \pi } \right)\)
- Khi vật ở VTCB : \(a = 0\)
- Khi vật ở vị trí biên : \(a = \pm {\omega ^2}A\)
Lời giải chi tiết:
a) Dựa vào đồ thị ta có :
Thời gian từ thời điểm thấp nhất đến điểm cao nhất : \(\frac{T}{2} = 0,2s = > T = 0,4s = > \omega = \frac{{2\pi }}{T} = 5\pi (rad/s)\)
Vận tốc cực đại của dao động :
\(v\max = A\omega = 30(m/s) = > A = \frac{{v\max }}{\omega } = \frac{6}{\pi }(cm)\)
Tại thời điểm t=0 , vật có v=vmax => vật ở VTCB và v > 0
=> x=0 => \(\cos \varphi = 0 = > \varphi = - \frac{\pi }{2}\)
Phương trình của vận tốc có dạng : \(v = A\omega \cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\)
\( = > v = \frac{6}{\pi }.5\pi \cos \left( {5\pi t - \frac{\pi }{2} + \frac{\pi }{2}} \right) = 30\cos \left( {5\pi t} \right)(cm/s)\)
b) Từ đồ thị ta có :
Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)
\( = > x = \frac{6}{\pi }\cos \left( {5\pi t - \frac{\pi }{2}} \right)(cm)\)
Phương trình của gia tốc có dạng : \(a = A{\omega ^2}\cos \left( {\omega t + \varphi + \pi } \right)\)
\( = > a = 150\pi \cos \left( {5\pi t + \frac{\pi }{2}} \right)(cm/{s^2})\)