Bài tập cuối chương II trang 27, 28, 29 SBT Vật lí 11 Kết nối tri thức với cuộc sống
Khi có sóng ngang truyền qua, các phần tử vật chất của môi trường dao động
II.1
Khi có sóng ngang truyền qua, các phần tử vật chất của môi trường dao động
A. theo phương song song với phương truyền sóng.
B. theo phương vuông góc với phương truyền sóng.
C. cùng pha với nhau.
D. với các tần số khác nhau.
Phương pháp giải:
Sử dụng khái niệm sóng ngang
Lời giải chi tiết:
Sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng gọi là sóng ngang.
Đáp án : B
II.2
Trường hợp nào sau đây là một ví dụ về sóng dọc?
A. Ánh sáng truyền trong không khí.
B. Sóng nước trên mặt hồ.
C. Sóng âm lan truyền trong không khí.
D. Sóng truyền một trên sợi dây.
Phương pháp giải:
Tính chất của sóng dọc .
Lời giải chi tiết:
Sóng dọc là sóng cơ, truyền được trong chất rắn, lỏng, khí
Đáp án : C
II.3
Tất cả các sóng điện từ đều có cùng
A. tốc độ khi truyền trong một môi trường nhất định.
B. tần số khi truyền trong môi trường chân không.
C. chu kì khi truyền trong một môi trường nhất định.
D. tốc độ khi truyền trong chân không.
Phương pháp giải:
Tính chất của sóng điện từ
Lời giải chi tiết:
Sóng điện từ truyền trong chân không bằng với vận tốc của ánh sáng \(c = {3.10^8}m/s\)
Đáp án : D
II.4
Hiện tượng giao thoa sóng xảy ra khi có
A. hai sóng chuyển động ngược chiều giao nhau.
B. hai sóng xuất phát từ hai tâm dao động cùng tần số, cùng pha giao nhau.
C. hai sóng dao động cùng phương, cùng pha giao nhau.
D. hai sóng xuất phát từ hai nguồn dao động cùng tần số.
Phương pháp giải:
Điều kiện xảy ra hiện tượng giao thoa sóng .
Lời giải chi tiết:
Điều kiện giao thoa sóng là hai nguồn sóng phải có : dao động cùng phương , cùng tần số và có độ lệch pha không đổi theo thời gian .
Đáp án : D
II.5
Sóng dừng là
A. sóng được tạo thành giữa hai điểm có định trong một môi trường.
B. sóng không lan truyền được do bị một vật cản chặn lại.
C. sóng được tạo thành do sự giao thoa của hai sóng kết hợp, trên đường thẳng nói hai tâm phát sóng.
D. Sóng được tạo thành do sự giao thoa giữa sóng tới và sóng phản xạ.
Phương pháp giải:
Khái niệm sóng dừng.
Lời giải chi tiết:
Hai sóng cùng biên độ, cùng tần số lan truyền theo hai hướng ngược nhau trên một dây giao thoa với nhau tạo nên một sóng tổng hợp gọi là sóng dừng
Đáp án : D
II.6
Một sóng vô tuyến được phát ra từ một đài phát thanh có bước sóng 3 m. Coi rằng tốc độ của sóng vô tuyến truyền trong không khí là \({3.10^8}\)m/s, tần số của sóng này là
A. \({10^{ - 8}}\) Hz.
B. \({9.10^{ - 8}}\) Hz.
C. \({10^8}\) Hz.
D. 9 Hz.
Phương pháp giải:
Bước sóng là khoảng cách giữa hai ngọn sóng liên tiếp :\(\lambda = v.T = \frac{v}{f}\)
Lời giải chi tiết:
Theo đề bài ta có : \(\lambda = \frac{v}{f} = 3m = > f = \frac{v}{\lambda } = \frac{{{{3.10}^8}}}{3} = {10^8}Hz\)
Đáp án : C
II.7
Người ta tạo ra sóng dừng trên một sợi dây căng giữa hai điểm cố định. Hai tần số gần nhau nhất cùng tạo ra sóng dừng trên dây là 150 Hz và 200 Hz. Tần số nhỏ nhất tạo ra sóng dừng trên dây đó là
A. 50 Hz.
B. 75 Hz.
C. 100 Hz.
D. 125 Hz.
Phương pháp giải:
Tính chất của sóng dừng
Lời giải chi tiết:
Theo đề bài ta có : \({f_1} = n{f_0} = 150\) và \({f_2} = \left( {n + 1} \right){f_0} = 200\) \( = > n = 3 = > {f_0} = 50Hz\)
Đáp án : A
II.8
Một sóng ngang có tần số 20 Hz truyền trên mặt nước với tốc độ 1,5 m/s. Trên phương truyền sóng, sóng truyền đến điểm P rồi mới đến điểm Q cách nó 16,125 cm. Tại thời điểm t, điểm P hạ xuống thấp nhất thì sau thời gian \(\Delta t = \frac{3}{{400}}s\), điểm Q sẽ tới vị trí nào?
Phương pháp giải:
Độ lệch pha giữa 2 điểm trên dây : \(\Delta \varphi = \frac{{2\pi d}}{\lambda }\)
Bước sóng của dao động : \(\lambda = v.T = \frac{v}{f}\)
Sử dụng vòng tròn lượng giác
Lời giải chi tiết:
Ta có : \(\lambda = \frac{v}{f} = \frac{{1,5}}{{20}} = 7,5cm\)
Chu kì \(T = \frac{1}{f} = \frac{1}{{20}} = 0,05s\)
Độ lệch pha giữa 2 điểm P và Q là : \(\Delta \varphi = \frac{{2\pi d}}{\lambda } = \frac{{2\pi .16,125}}{{7,5}} = \frac{{43\pi }}{{10}} = 4\pi + \frac{{3\pi }}{{10}}\)
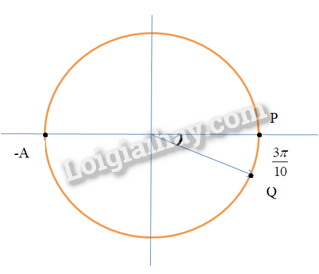
=> P sớm pha hơn Q một góc \(\varphi = \frac{{3\pi }}{{10}}\)
Tại thời điểm t, điểm P hạ xuống thấp nhất thì sau thời gian \(\Delta t = \frac{3}{{400}}s = \frac{{3T}}{{20}}\), điểm Q sẽ tới vị trí biên dương
II.9
Trong thí nghiệm Young về giao thoa với ánh sáng đơn sắc có bước sóng \(\lambda \). Biết khoảng cách giữa hai khe là 1 mm. Tại điểm M cách vân sáng trung tâm 1,2 mm trên màn quan sát là vị trí vân sáng bậc 4. Nếu dịch màn ra xa thêm một đoạn 25 cm theo phương vuông góc với mặt phẳng hai khe thì tại M là vị trí vân sáng bậc 3. Bước sóng \(\lambda \) dùng trong thí nghiệm là
A. 0,4 \(\mu m\)
B. 0,5\(\mu m\).
C. 0,6\(\mu m\).
D. 0,64 \(\mu m\).
Phương pháp giải:
Áp dụng công thức tính khoảng vân: \(i = \frac{{\lambda D}}{a}\)
Sử dụng lí thuyết khoảng cách giữa hai vân sáng liên tiếp bằng khoảng vân i
Lời giải chi tiết:
Tại điểm M cách vân sáng trung tâm 1,2 mm trên màn quan sát là vị trí vân sáng bậc 4 => \(4i = \frac{{4\lambda D}}{a} = 1,2mm\)
Nếu dịch màn ra xa thêm một đoạn 25 cm theo phương vuông góc với mặt phẳng hai khe thì tại M là vị trí vân sáng bậc 3 => \(3{i'} = \frac{{3\lambda \left( {D + 0,25} \right)}}{a}\)
Theo đề bài ta có : \(4i = 3{i'} = > 4D = 3\left( {D + 0,25} \right) \Leftrightarrow D = 0,75m\)
Ta có : \(4i = \frac{{4\lambda D}}{a} = 1,2mm = > \lambda = 0,4\mu m\)
Đáp án : A
II.10
Hình II.1 mô tả đồ thị li độ - thời gian của một sóng.
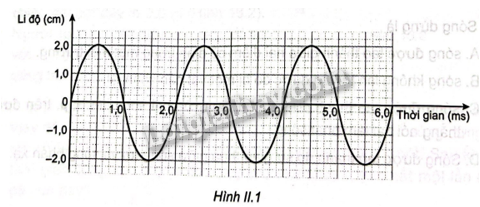
a) Tính chu kì, tần số và biên độ của sóng.
b) Biết tốc độ của sóng là 5 m/s, tính bước sóng.
Phương pháp giải:
Đồ thị dao động
Lời giải chi tiết:
a) Từ đồ thị ta có
Biên độ dao động của vật : \(A = x\max = 2(cm)\)
Từ vị trí thấp nhất đến vị trí cao nhất là \(\frac{T}{2} = 0,001 = > T = 0,002(s) = > f = \frac{1}{T} = 500Hz\)
b) Biết tốc độ của sóng là 5 m/s, bước sóng \(\lambda = \frac{v}{f} = \frac{5}{{500}} = 0,01m = 1cm\)
II.11
Hình II.2 cho thấy các phần tử chính của thang sóng điện từ.

a) Nêu ba đặc điểm chung của các sóng điện từ.
b) Sóng lò vi sóng có tốc độ \({3.10^8}\)m/s trong chân không và tần số \(1,{5.10^{10}}\)Hz. Tính bước sóng của sóng này.
c) Hãy gọi tên của các sóng điện từ nằm trong vùng A, B, C, D trên Hình II.2.
Phương pháp giải:
Sử dụng thang sóng điện từ
Dựa vào tính chất của sóng điện từ.
Lời giải chi tiết:
a) Ba đặc điểm chung của các sóng điện từ :
- Lan truyền được trong các môi trường rắn, lỏng, khí và chân không. Là sóng duy nhất lan truyền được trong chân không.
- Tốc độ lan truyền sóng điện từ trong chân không là lớn nhất và bằng c = 3.10 8 m/s.
- Tốc độ lan truyền sóng điện từ trong chân không là lớn nhất và bằng c = 3.10 8 m/s.
b) Sóng lò vi sóng có tốc độ \({3.10^8}\)m/s trong chân không và tần số \(1,{5.10^{10}}\)Hz => bước sóng \(\lambda = \frac{v}{f} = \frac{{{{3.10}^8}}}{{1,{{5.10}^{10}}}} = 0,02m = 2cm\)
c) Sóng điện từ nằm trong vùng
A là tia X
B là tia tử ngoại
C là tia hồng ngoại
D là vi sóng
II.12
Một sợi dây đàn hồi, mảnh, dài có đầu O dao động với tần số f thay đổi được trong khoảng từ 80 Hz đền 125 Hz, theo phương vuông góc với sợi dây. Sóng tạo thành lan truyền trên dây với tốc độ không đổi v = 10 m/s.
a) Cho f = 80 Hz, tính chu kì và bước sóng của sóng trên dây.
b) Tính tần số f để điểm M trên dây cách O một khoảng bằng 20 cm luôn dao động cùng pha với O.
Phương pháp giải:
Những điểm cách nguồn một khoảng bằng \(k\lambda \)thì dao động đồng pha với nguồn
Lời giải chi tiết:
Theo đề bài ta có : \(f = 80Hz = > T = \frac{1}{f} = 0,0125s\)
Bước sóng của sóng trên dây \(\lambda = \frac{v}{f} = \frac{{10}}{{80}} = 0,125m\)
điểm M trên dây cách O một khoảng bằng 20 cm luôn dao động cùng pha với O nên ta có \(k\lambda = 0,2 = k\frac{v}{f} = > f = \frac{{kv}}{{0,2}} = > 80 \le \frac{{k.10}}{{0,2}} \le 125 = > 80 \le 50k \le 125 = > 1,6 \le k \le 2,5 = > k = 2\)
\( = > k\frac{v}{f} = 0,2 = > f = \frac{{kv}}{{0,2}} = \frac{{2.10}}{{0,2}} = 100Hz\)
II.13
Một người leo núi khi cách vách núi một khoảng 450 m (Hình II.3), người này hét một tiếng lớn và âm phản xạ trở lại tai người sau 2,75 s.
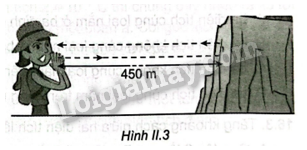
a) Tính tốc độ truyền sóng âm.
b) Nếu sóng âm trên có bước sóng là 0,75 m thì tần số của sóng là bao nhiêu?
Phương pháp giải:
Tính chất của sóng âm ;
Lời giải chi tiết:
a) Người này hét một tiếng lớn và âm phản xạ trở lại tai người sau 2,75 s => \(t = \frac{{{t'}}}{2} = \frac{{2,75}}{2} = 1,375s\)
Tốc độ truyền sóng âm \(v = \frac{S}{t} = \frac{{450}}{{1,375}} = 327m/s\)
b) Nếu sóng âm trên có bước sóng là 0,75 m thì tần số của sóng là \(f = \frac{v}{\lambda } = \frac{{327}}{{0,75}} = 436Hz\)
II.14
Sóng vô tuyến ngắn có thể được sử dụng để đo khoảng cách từ Trái Đất đến Mặt Trăng, bằng cách phát một tín hiệu từ Trái Đất tới Mặt Trăng và thu tín hiệu trở lại, đo khoảng thời gian từ khi phát đến khi nhận tín hiệu.
a) Biết khoảng thời gian từ khi phát tới khi nhận được tín hiệu trở lại là 2,6 s.
Tính khoảng cách từ Mặt Trăng tới Trái Đất.
b) Sóng vô tuyến trên có tần số \({10^7}\) Hz. Tính bước sóng của sóng.
Phương pháp giải:
Bước sóng là khoảng cách giữa hai ngọn sóng liên tiếp :\(\lambda = v.T = \frac{v}{f}\)
Lời giải chi tiết:
Thời gian truyền đi \(t = \frac{{{t'}}}{2} = \frac{{2,6}}{2} = 1,3s\)
Khoảng cách từ Mặt Trăng tới Trái Đất \(S = v.t = {3.10^8}.1,3 = 3,{9.10^8}m\)
Sóng vô tuyến trên có tần số \({10^7}\) Hz => bước sóng của sóng : \(\lambda = \frac{v}{f} = \frac{{{{3.10}^8}}}{{{{10}^7}}} = 30m\)
II.15
Trong thí nghiệm Young về giao thoa với ánh sáng đơn sắc. Trên màn chỉ quan sát được 21 vạch sáng mà khoảng cách giữa hai vạch sáng ngoài cùng là 4 cm, Tại hai điểm P và Q là hai vị trí cho vân sáng trên màn. Hãy xác định số vân sáng trên đoạn PQ, biết rằng khoảng cách giữa hai điểm đó là 2,4 cm.
Phương pháp giải:
Áp dụng công thức tính khoảng vân: \(i = \frac{{\lambda D}}{a}\)
Sử dụng lí thuyết khoảng cách giữa hai vân sáng liên tiếp bằng khoảng vân i
Lời giải chi tiết:
Trên màn chỉ quan sát được 21 vạch sáng ứng vớu 20 khoảng vân => \(20i = 4cm = > i = 0,2cm\)
Tại hai điểm P và Q là hai vị trí cho vân sáng trên màn, biết rằng khoảng cách giữa hai điểm đó là 2,4 cm \( = > ki = 2,4 = > k = \frac{{2,4}}{i} = \frac{{2,4}}{{0,2}} = 12\)
Vậy có 13 vân sáng trên PQ