Giải SBT Vật lý 11 Chủ đề 2. Sóng - Cánh diều — Không quảng cáo

Mô tả sóng 2.1

Khoảng cách giữa hai điểm gần nhất trên cùng một phương truyền sóng dao động cùng pha là

A. bước sóng.

B. tần số sóng.

C. biên độ sóng.

D. chu kì sóng.

Phương pháp giải:

Vận dụng kiến thức đã học về bước sóng λ: là quãng đường mà sóng truyền đi trong một chu kì sóng, là khoảng cách giữa hai điểm gần nhất trên cùng một phương truyền sóng dao động cùng pha.

Lời giải chi tiết:

Đáp án: A. bước sóng.

Mô tả sóng 2.2

Tốc độ sóng là

A. tốc độ dao động của điểm sóng.

B. tốc độ lan truyền của phần tử môi trường.

C. tốc độ lan truyền năng lượng của sóng trong không gian.

D. tốc độ lan truyền của điểm sóng trong không gian.

Phương pháp giải:

Vận dụng kiến thức đã học về tốc độ sóng: là tốc độ lan truyền năng lượng của sóng trong không gian và được xác định theo công thức: v = fλ .

Lời giải chi tiết:

Đáp án: C. tốc độ lan truyền năng lượng của sóng trong không gian.

Mô tả sóng 2.3

Một sóng cơ lan truyền trong một môi trường với tốc độ 1,0 m/s và tần số 10 Hz, biên độ sóng không đổi. Trong khoảng thời gian giữa hai lần liên tiếp khi một phần tử của môi trường ở vị trí cân bằng, sóng lan truyền được quãng đường là:

A. 4 cm.

B. 10 cm.

C. 8 cm.

D. 5 cm.

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng của sóng:

- Bước sóng λ là quãng đường mà sóng truyền đi trong một chu kì sóng.

- Tốc độ sóng là tốc độ lan truyền năng lượng của sóng trong không gian: v = fλ.

Lời giải chi tiết:

Bước sóng \(\lambda {\rm{ = }}\frac{v}{f}{\rm{ = }}\frac{1}{{10}}{\rm{ = 0,1 m}}\)

Quãng đường giữa hai VTCB liên tiếp là \(s = \frac{\lambda }{2}{\rm{ = }}\frac{{0,1}}{2}{\rm{ = 0,05 m  =  5 cm}}\)

Mô tả sóng 2.4

Hiệu ứng Doppler là hiện tượng khi người quan sát chuyển động lại gần nguồn phát thì

A. tần số sóng thu được nhỏ hơn tần số sóng của nguồn phát.

B. tần số sóng thu được lớn hơn tần số sóng của nguồn phát.

C. tần số sóng thu được bằng tần số sóng của nguồn phát.

D. tần số sóng thu được lúc đầu nhỏ hơn, lúc sau lớn hơn tần số sóng của nguồn phát.

Phương pháp giải:

Vận dụng kiến thức đã học về hiệu ứng Doppler: Hiệu ứng Doppler là hiện tượng khi người quan sát chuyển động lại gần nguồn phát thì tần số sóng thu được lớn hơn tần số sóng của nguồn phát và khi người quan sát chuyển động ra xa thì ngược lại.

Lời giải chi tiết:

Đáp án: B. tần số sóng thu được lớn hơn tần số sóng của nguồn phát.

Mô tả sóng 2.5

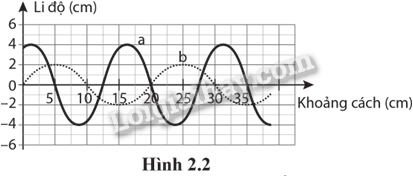Xác định bước sóng và biên độ của các sóng a và b được mô tả trong đồ thị li độ – khoảng cách trên Hình 2.2.

Phương pháp giải:

Áp dụng kiến thức về tần số f : là số dao động mà vật thực hiện được trong một giây.

Lời giải chi tiết:

Sóng a có bước sóng λ _a = 15 cm; biên độ A _a = 4 cm.

Sóng b có bước sóng λ _b = 20 cm; biên độ A _b = 2 cm.

Mô tả sóng 2.6

Sử dụng hệ toạ độ li độ – khoảng cách, hãy vẽ đồ thị của hai sóng C và D trong đó sóng C có biên độ và bước sóng gấp đôi biên độ và bước sóng của sóng D.

Phương pháp giải:

Vận dụng kiến thức đã học về đồ thị li độ – khoảng cách và các đại lượng của sóng.

- Biên độ sóng A là độ lớn cực đại của li độ của một điểm sóng.

- Chu kì sóng T là thời gian vật thực hiện môt dao động của một điểm sóng.

- Tần số sóng f là số dao động mà mỗi điểm sóng thực hiện được trong một đơn vị thời gian: \(f = \frac{1}{T}\)

Lời giải chi tiết:

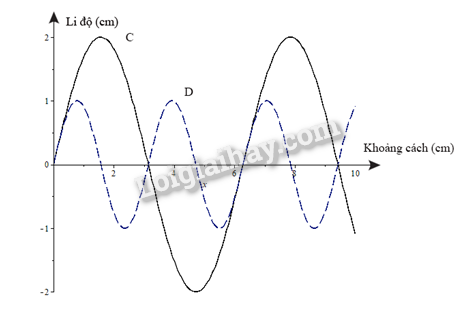
Mô tả sóng 2.7

Nốt đô trung (C4) của một đàn piano trong dàn nhạc giao hưởng có tần số 264 Hz.

a) Xác định chu kì và bước sóng của sóng âm của nốt này. Biết tốc độ truyền âm trong không khí là 330 m/s.

b) Dao động của hai phần tử môi trường không khí trên cùng một phương truyền sóng của sóng này có cùng pha không nếu chúng cách nhau 1,25 m? 2,50 m?

Phương pháp giải:

Vận dụng kiến thức về các đại lượng của sóng:

- Tần số sóng f là số dao động mà mỗi điểm sóng thực hiện được trong một đơn vị thời gian: \(f = \frac{1}{T}\)

- Tốc độ sóng v là tốc độ lan truyền năng lượng của sóng trong không gian: v = fλ.

- Chu kì sóng T : là thời gian vật thực hiện môt dao động của một điểm sóng: \(T = \frac{1}{f}\)

- Bước sóng λ là quãng đường mà sóng truyền đi trong một chu kì sóng: \(\lambda  = \frac{v}{f}\)

- Trong cùng một phương truyền sóng, khoảng cách giữa hai dao động là d :

+ \(d = k\lambda \left( {k \in N} \right):\) Hai dao động cùng pha.

+ \(d = \left( {k + \frac{1}{2}} \right)\lambda \left( {k \in N} \right):\) Hai dao động ngược pha.

+ \(d = \frac{\lambda }{4}\left( {k \in N} \right):\) Hai dao động vuông pha.

Lời giải chi tiết:

a) Chu kì của sóng âm này là: \(T = \frac{1}{f}{\rm{ = }}\frac{1}{{264}}{\rm{ = 3,79}}{\rm{.1}}{{\rm{0}}^{ - 3}}{\rm{ s}}\)

Bước sóng của sóng âm này là: \(\lambda  = \frac{v}{f}{\rm{ = }}\frac{{330}}{{264}}{\rm{ = }}1,25{\rm{ m}}\)

b) Hai phần tử môi trường cách nhau 1,25 m = λ thì dao động cùng pha. Hai phần tử môi trường cách nhau 2,50 m = 2λ thì cũng dao động cùng pha.

Mô tả sóng 2.8

Một sóng có biên độ 5,00 cm và cường độ tương ứng là 200 W/m ² . Biết cường độ sóng tỉ lệ thuận với bình phương biên độ sóng. a) Nếu biên độ của sóng nói trên tăng lên thành 10,00 cm thì cường độ của sóng là bao nhiêu? b) Nếu cường độ của sóng giảm xuống còn 100 W/m ² thì biên độ tương ứng là bao nhiêu?

Phương pháp giải:

Vận dụng kiến thức về các đại lượng của sóng:

- Biên độ sóng A là độ lớn cực đại của li độ của một điểm sóng.

- Cường độ sóng I là năng lượng truyền qua một đơn vị diện tích vuông góc với phương truyền sóng trong một đơn vị thời gian: \(I = \frac{E}{{St}}\)

Lời giải chi tiết:

a) Biên độ của sóng nói trên tăng lên thành 10,00 cm là tăng biên độ lên gấp đôi.

Cường độ của sóng đó là I = 200.4 = 800 W/m ²

b) Cường độ của sóng giảm xuống còn 100 W/m ² là giảm xuống một nửa.

Biên độ của sóng lúc này là \(A = \frac{5}{{\sqrt 2 }}{\rm{ = 3}},54{\rm{ cm}}\)

Mô tả sóng 2.9

Một bóng đèn công suất 100 W phát ra ánh sáng theo mọi phương. Coi bóng đèn là một điểm, hãy xác định cường độ sóng gây ra bởi bóng đèn tại một điểm cách bóng đèn 2,00 m.

Phương pháp giải:

Vận dụng kiến thức về các đại lượng của sóng:

- Cường độ sóng I là năng lượng truyền qua một đơn vị diện tích vuông góc với phương truyền sóng trong một đơn vị thời gian: \(I = \frac{E}{{St}}\)

- Công suất là năng lượng E phát ra trong một đơn vị thời gian.

Lời giải chi tiết:

Công suất đèn chính là năng lượng mỗi giây truyền qua diện tích mặt cầu có tâm là bóng đèn, bán kính là khoảng cách từ đèn đến điểm cần xác định cường độ sóng.

Diện tích mặt cầu sóng truyền qua: S = 4π R ² = 4π2 ² = 50,3 m ²

Cường độ sóng gây ra bởi bóng đèn tại một điểm cách bóng đèn 2,00 m là:

\(I = \frac{P}{S} = \frac{{100}}{{50,3}}{\rm{ = 1}},99{\rm{ W}}/{{\rm{m}}^2}\)

Sóng dọc và sóng ngang 2.10

Các điểm sóng dọc có phương dao động

A. nằm ngang.

B. trùng với phương truyền sóng.

C. vuông góc với phương truyền sóng.

D. thẳng đứng.

Phương pháp giải:

Vận dụng kiến thức đã học về sóng dọc: là sóng có các phần tử dao động theo phương truyền sóng. Sóng âm trong không khí là một sóng dọc.

Lời giải chi tiết:

Đáp án: B. trùng với phương truyền sóng.

Sóng dọc và sóng ngang 2.11

Sóng trên mặt nước là sóng ngang. Một người quan sát thấy một chiếc phao trên mặt biển nhô lên cao 10,0 lần trong 36,0 giây và đo được khoảng cách hai đỉnh lân cận là 10,0 m. Tốc độ truyền sóng trên mặt biển là:

A. 2,5 m/s.

B. 5,00 m/s.

C. 10,0 m/s.

D. 1,25 m/s.

Phương pháp giải:

Vận dụng kiến thức về các đại lượng của sóng:

- Sóng ngang có các phần tử dao động theo phương vuông góc với phương truyền sóng. Sóng trên mặt nước là một sóng ngang.

- Chu kì sóng T là thời gian thực hiện một dao động của một điểm sóng. Tần số sóng  f  là số dao động mà mỗi điểm sóng thực hiện trong một đơn vị thời gian:\(f = \frac{1}{T}\)

- Bước sóng λ là quãng đường mà sóng truyền đi trong một chu kì sóng.

- Tốc độ sóng là tốc độ lan truyền năng lượng của sóng trong không gian và được xác định theo công thức: v = fλ

Lời giải chi tiết:

Chu kì của sóng: T = 36/9 = 4 s.

Bước sóng λ = 10 m.

Tốc độ truyền sóng trên mặt biển: \(v = \frac{\lambda }{T} = \frac{{10}}{4}{\rm{ = 2,5 m/s}}\)

Sóng dọc và sóng ngang 2.12

Để phân loại sóng dọc và sóng ngang, người ta dựa vào

A. tốc độ truyền sóng và bước sóng.

B. phương truyền sóng và tần số sóng.

C. phương dao động và phương truyền sóng.

D. phương dao động và tốc độ truyền sóng.

Phương pháp giải:

Vận dụng kiến thức đã học về hai loại sóng:

- Sóng dọc là sóng có các phần tử dao động theo phương truyền sóng. Sóng âm trong không khí là một sóng dọc.

- Sóng ngang có các phần tử dao động theo phương vuông góc với phương truyền sóng. Sóng trên mặt nước là một sóng ngang.

Lời giải chi tiết:

Đáp án: C. phương dao động và phương truyền sóng.

Sóng dọc và sóng ngang 2.13

Âm thanh là sóng dọc có thể lan truyền qua các môi trường rắn. Tính tần số của một sóng âm có bước sóng 0,250 m truyền qua một tấm thép với tốc độ 5 060 m/s.

Phương pháp giải:

Vận dụng kiến thức về các đại lượng của sóng:

- Tần số sóng  f  là số dao động mà mỗi điểm sóng thực hiện trong một đơn vị thời gian:\(f = \frac{1}{T}\)

- Bước sóng λ là quãng đường mà sóng truyền đi trong một chu kì sóng.

- Tốc độ sóng là tốc độ lan truyền năng lượng của sóng trong không gian và được xác định theo công thức: v = fλ

Lời giải chi tiết:

Tần số của sóng âm này là: \(f = \frac{v}{\lambda } = \frac{{5060}}{{0,25}}{\rm{ = 20,2}}{\rm{.1}}{{\rm{0}}^3}{\rm{ Hz}}\)

Sóng dọc và sóng ngang 2.14

Một sóng âm được hiển thị trên màn của một dao động kí điện tử như Hình 2.3. Bộ điều chỉnh thời gian được đặt sao cho giá trị của mỗi độ chia trên màn hình là 0,005 s. Xác định tần số của sóng âm.

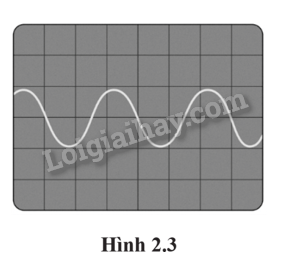
Phương pháp giải:

Vận dụng kiến thức đã học về đồ thị li độ – khoảng cách và các đại lượng của sóng.

- Biên độ sóng A là độ lớn cực đại của li độ của một điểm sóng.

- Chu kì sóng T : Thời gian vật thực hiện môt dao động của một điểm sóng.

- Tần số sóng: Số dao động mà mỗi điểm sóng thực hiện được trong một đơn vị thời gian: \(f = \frac{1}{T}\)

Lời giải chi tiết:

Từ hình 2.3, chu kì của sóng âm là T = 0,005.3 = 0,015 s

Tần số của sóng âm là \(f = \frac{1}{T} = \frac{1}{{0,015}}{\rm{ = 67 Hz}}\)

Sóng dọc và sóng ngang 2.15

Hãy nghiên cứu bảng bên về tần số các miền bức xạ điện từ và trả lời các câu hỏi sau:

a) Miền bức xạ nào có khoảng giá trị bước sóng hẹp nhất?

b) Bước sóng của ánh sáng nằm trong khoảng giá trị nào theo đơn vị mm?

Phương pháp giải:

Vận dụng các kiến thức về sóng:

- Thang sóng điện từ được chia thành các vùng gồm: sóng vô tuyến, hồng ngoại, ánh sáng khả kiến, tử ngoại, tia X, tia gamma. Ánh sáng là sóng điện từ.

- Trong chân không, tất cả sóng điện từ đều truyền với tốc độ c = 3.10 ⁸ m/s

Lời giải chi tiết:

a) Miền bức xạ có khoảng giá trị bước sóng hẹp nhất là tia gamma. b) Bước sóng ánh sáng đỏ: λ _d = 8.10 ^-7 m = 8.10 ^-4 mm. Bước sóng ánh sáng tím: λ _t = 4.10 ^-7 m = 4.10 ^-4 mm.

Sóng dọc và sóng ngang 2.16

Mỗi bức xạ điện từ tương ứng với các tần số: 200 kHz, 100 MHz, 5.10 ¹⁴ Hz, 10 ¹⁸ Hz thuộc loại bức xạ điện từ nào? Xác định bước sóng của mỗi bức xạ điện từ đó khi đo trong chân không.

Phương pháp giải:

Vận dụng các kiến thức về sóng:

- Thang sóng điện từ được chia thành các vùng gồm: sóng vô tuyến, hồng ngoại, ánh sáng khả kiến, tử ngoại, tia X, tia gamma. Ánh sáng là sóng điện từ.

- Trong chân không, tất cả sóng điện từ đều truyền với tốc độ c = 3.10 ⁸ m/s

Lời giải chi tiết:

Bức xạ điện từ tần số 200 kHz là sóng vô tuyến có bước sóng λ = 1500 m.

Bức xạ điện từ tần số 100 MHz là sóng vô tuyến có bước sóng λ = 3 m.

Bức xạ điện từ tần số 5.10 ¹⁴ Hz là ánh sáng có bước sóng λ = 6.10 ^–7 m.

Bức xạ điện từ tần số 10 ¹⁸ Hz là tia X có bước sóng λ = 3.10 ^–10 m.

Sóng dọc và sóng ngang 2.17

Hoàn thiện các số liệu còn thiếu trong bảng sau về một số sóng vô tuyến.

Phương pháp giải:

Vận dụng các kiến thức về sóng:

- Thang sóng điện từ được chia thành các vùng gồm: sóng vô tuyến, hồng ngoại, ánh sáng khả kiến, tử ngoại, tia X, tia gamma. Ánh sáng là sóng điện từ.

- Trong chân không, tất cả sóng điện từ đều truyền với tốc độ c = 3.10 ⁸ m/s

Lời giải chi tiết:

Sóng dọc và sóng ngang 2.18

Khi ánh sáng đỏ (có bước sóng 7,0.10 ^–7 m trong chân không) truyền vào trong thuỷ tinh, tốc độ của nó giảm xuống còn 2,0.10 ⁸ m/s. Hãy xác định:

a) Tần số của ánh sáng đỏ trong chân không.

b) Tần số và bước sóng của ánh sáng này trong thuỷ tinh.

Phương pháp giải:

Vận dụng các kiến thức về sóng:

- Thang sóng điện từ được chia thành các vùng gồm: sóng vô tuyến, hồng ngoại, ánh sáng khả kiến, tử ngoại, tia X, tia gamma. Ánh sáng là sóng điện từ.

- Trong chân không, tất cả sóng điện từ đều truyền với tốc độ c = 3.10 ⁸ m/s

- Tốc độ sóng là tốc độ lan truyền năng lượng của sóng trong không gian và được xác định theo công thức: v = fλ

Lời giải chi tiết:

a) Tần số của ánh sáng đỏ trong chân không là: \(f = \frac{c}{\lambda } = \frac{{{{3.10}^8}}}{{{{7.10}^{ - 7}}}}{\rm{  = 4,3}}{\rm{.1}}{{\rm{0}}^{14}}{\rm{ Hz}}\) b) Trong thủy tinh, tần số của ánh sáng không đổi: f = 4,3.10 ¹⁴ Hz.

Bước sóng của ánh sáng này trong thuỷ tinh là:\(\lambda  = \frac{v}{f} = \frac{{{{2.10}^8}}}{{4,{{3.10}^{14}}}} = 4,{7.10^{ - 7}}{\rm{ m}}\)

Sóng dọc và sóng ngang 2.19

Một sóng dọc khi lan truyền trong không khí gây ra sự giãn/nén của các phân tử khí theo phương truyền sóng. Sóng này có thể được biểu diễn bằng mô hình sóng trên đồ thị li độ – khoảng cách như Hình 2.4. Các vùng giãn và nén trên hình sẽ thay đổi như thế nào sau 1/2 chu kì? Hãy biểu diễn các vùng đó.

Phương pháp giải:

Vận dụng kiến thức đã học về đồ thị li độ – khoảng cách và các đại lượng của sóng.

- Biên độ sóng A là độ lớn cực đại của li độ của một điểm sóng.

- Chu kì sóng T : Thời gian vật thực hiện môt dao động của một điểm sóng.

Lời giải chi tiết:

Sau 1/2 chu kì, đồ thị li độ – thời gian theo mô hình sóng của sóng dọc sẽ dịch đi một đoạn bằng 1/2 bước sóng. Đối chiếu vùng nén tương ứng với biểu diễn li độ cực đại và vùng giãn với li độ cực tiểu, ta biểu diễn được các vùng nén, giãn của các phân tử khí sau 1/2 chu kì như hình vẽ sau.

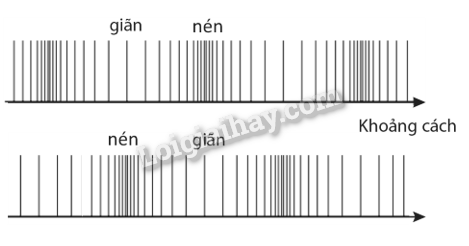
Sóng dọc và sóng ngang 2.20

Hãy xác định mỗi sóng sau đây là sóng ngang hay sóng dọc: a) Sóng trên dây đàn ghita được gảy. b) Sóng âm được tạo ra bởi một dây đàn ghita đang rung. c) Sóng trên một lò xo với đầu lò xo có thể di chuyển tới lui dọc theo chiều dài của lò xo.

Phương pháp giải:

Vận dụng kiến thức đã học về các loại sóng:

- Sóng dọc là sóng có các phần tử dao động theo phương truyền sóng. Sóng âm trong không khí là một sóng dọc. - Sóng ngang có các phần tử dao động theo phương vuông góc với phương truyền sóng. Sóng trên mặt nước là một sóng ngang.

Lời giải chi tiết:

a) Sóng trên dây đàn ghita được gảy là sóng ngang. b) Sóng âm được tạo ra bởi một dây đàn ghita đang rung là sóng dọc. c) Sóng trên một lò xo với đầu lò xo có thể di chuyển tới lui dọc theo chiều dài của lò xo là sóng dọc.

Giao thoa sóng 2.21

Điều kiện có giao thoa sóng là gì?

A. Có hai sóng chuyển động ngược chiều giao nhau.

B. Có hai sóng cùng tần số và có độ lệch pha không đổi.

C. Có hai sóng cùng bước sóng giao nhau.

D. Có hai sóng cùng biên độ, cùng tốc độ giao nhau.

Phương pháp giải:

Vận dụng kiến thức đã học về giao thoa: là hiện tượng hai sóng kết hợp gặp nhau tại những điểm xác định tạo nên những điểm dao động với biên độ cực đại (hai sóng tăng cường lẫn nhau) và những điểm dao động với biên độ cực tiểu (hai sóng làm suy yếu lẫn nhau).

Lời giải chi tiết:

Đáp án: B. Có hai sóng cùng tần số và có độ lệch pha không đổi.

Giao thoa sóng 2.22

Trong thí nghiệm giao thoa sóng trên mặt nước, hai nguồn A, B dao động cùng pha với cùng tần số f = 13 Hz. Tại một điểm M cách các nguồn A, B lần lượt là d ₁ = 19 cm, d ₂ = 21 cm thì sóng có biên độ cực đại. Giữa M và đường trung trực của AB không có dãy cực đại khác. Tốc độ truyền sóng trên mặt nước là:

A. v = 26 m/s.

B. v = 52 m/s.

C. v = 26 cm/s.

D. v = 52 cm/s.

Phương pháp giải:

Vận dụng kiến thức đã học về giao thoa sóng nước:

- Giao thoa là hiện tượng hai sóng kết hợp gặp nhau tại những điểm xác định tạo nên những điểm dao động với biên độ cực đại (hai sóng tăng cường lẫn nhau) và những điểm dao động với biên độ cực tiểu (hai sóng làm suy yếu lẫn nhau). - Trong giao thoa sóng nước, các điểm dao động với biên độ cực đại hay cực tiểu nằm trên các đường xác định xen kẽ trên mặt nước. Những điểm dao động với biên độ cực đại là những điểm mà hiệu đường đi của sóng từ hai nguồn đến điểm đó bằng nguyên lần bước sóng: \({x_2}--{\rm{ }}{x_1} = k\lambda \) - Những điểm dao động với biên độ cực tiểu:\({x_2}--{\rm{ }}{x_1} = \left( {k + \frac{1}{2}} \right)\lambda \)

- Tốc độ sóng là tốc độ lan truyền năng lượng của sóng trong không gian và được xác định theo công thức: v = fλ

Lời giải chi tiết:

Bước sóng của hai nguồn là: λ = d ₂ - d ₁ = 21 – 19 = 2 cm

Tốc độ truyền sóng trên mặt nước là: v = λ f = 2.13 = 26 cm/s

Giao thoa sóng 2.23

Trong thí nghiệm Young về giao thoa ánh sáng, hai khe cách nhau a = 0,5 mm và được chiếu sáng bằng ánh sáng đơn sắc có bước sóng λ . Khoảng cách từ hai khe đến màn quan sát là 2 m. Trên màn quan sát, trong vùng giữa hai điểm M và N mà MN = 2 cm, người ta thấy tại M và N đều là vân sáng và đếm được có 10 vân tối. Bước sóng λ của ánh sáng dùng trong thí nghiệm này là:

A. 0,4 μm.

B. 0,5 μm.

C. 0,6 μm.

D. 0,7 μm.

Phương pháp giải:

Vận dụng kiến thức đã học về thí nghiệm về giao thoa ánh sáng với hai khe sáng hẹp của Young, các vân sáng, vân tối nằm xen kẽ và cách đều nhau trên màn quan sát. Khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp được gọi là khoảng vân và tính bằng công thức: \(i = \frac{{\lambda D}}{a}\)

Lời giải chi tiết:

Ta có, khoảng vân \(i = \frac{{MN}}{{10}} = \frac{2}{{10}} = 0,2{\rm{ cm  =  2 mm}}\)

Bước sóng λ của ánh sáng này là: \(\lambda  = \frac{{ia}}{D} = \frac{{2.0,5}}{2} = 0,5{\rm{ \mu m}}\)

Giao thoa sóng 2.24

Trên giấy kẻ ô vuông, vẽ hai “sóng tam giác” giống như trong Hình 2.5. Xác định li độ tổng hợp tại các điểm thích hợp của sóng và vẽ đường biểu diễn sóng tổng hợp.

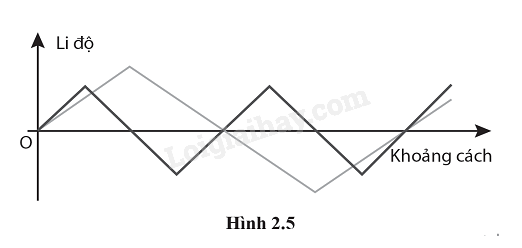
Phương pháp giải:

Vận dụng kiến thức đã học về đồ thị li độ – khoảng cách và các đại lượng của sóng.

- Biên độ sóng A là độ lớn cực đại của li độ của một điểm sóng.

- Chu kì sóng T : Thời gian vật thực hiện môt dao động của một điểm sóng.

- Tần số sóng: Số dao động mà mỗi điểm sóng thực hiện được trong một đơn vị thời gian: \(f = \frac{1}{T}\)

- Khi tổng hợp hai dao động, li độ của dao động chỉ bằng tổng hai li độ khi hai dao động hợp thành thực hiện theo một phương.

Lời giải chi tiết:

Xác định li độ của sóng tổng hợp là kết quả cộng đại số giá trị li độ của hai sóng thành phần tại các điểm gấp khúc của đồ thị mỗi sóng. Đường nối các điểm đó cho đường biểu diễn sóng tổng hợp của hai “sóng tam giác” như đường (3) trong hình vẽ sau.

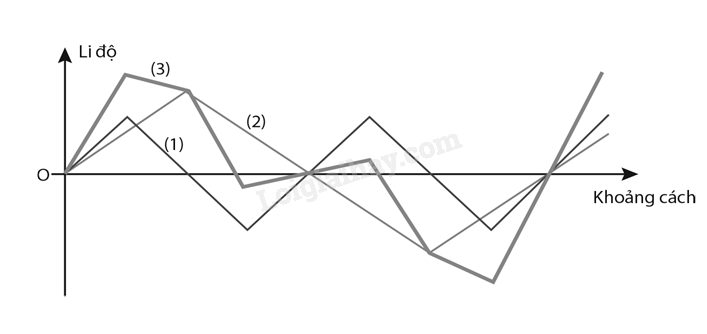
Giao thoa sóng 2.25

Hai sóng cùng tần số, có biên độ lần lượt là 0,20 m và 0,10 m truyền theo cùng một hướng. Vẽ phác hoạ đồ thị li độ – thời gian để minh hoạ những trường hợp sau đây: a) Hai sóng cùng pha với nhau. b) Hai sóng lệch pha nhau 90 ^o .

Phương pháp giải:

Vận dụng kiến thức đã học về đồ thị li độ – khoảng cách và biên độ của hai nguồn giao thoa:

- Biên độ sóng A là độ lớn cực đại của li độ của một điểm sóng.

- Chu kì sóng T : Thời gian vật thực hiện môt dao động của một điểm sóng.

- Tần số sóng: Số dao động mà mỗi điểm sóng thực hiện được trong một đơn vị thời gian: \(f = \frac{1}{T}\)

- Biên độ dao động tổng hợp tại điểm M do hai nguồn giao thoa truyền tới với cùng phương truyền sóng: \({A_M} = 2A\left| {\cos \left( {\pi \frac{{{d_1} - {d_2}}}{\lambda } + \frac{{{\varphi _2} - {\varphi _1}}}{2}} \right)} \right|\)

+ Hai sóng cùng pha:

A _{Mm ax} = 2 A khi d ₂ – d ₁ = k λ \(\left( {k \in Z} \right)\)

A _Mmin = 0 khi \({d_2}--{\rm{ }}{d_1} = \left( {k + \frac{1}{2}} \right)\lambda {\rm{ }}\left( {k \in Z} \right)\)

+ Hai sóng vuông pha:

A _{Mm ax} = 2 A khi \({d_2}--{\rm{ }}{d_1} = \left( {k + \frac{1}{4}} \right)\lambda {\rm{ }}\left( {k \in Z} \right)\)

A _Mmin = 0 khi \({d_2}--{\rm{ }}{d_1} = \left( {k + \frac{3}{4}} \right)\lambda {\rm{ }}\left( {k \in Z} \right)\)

Lời giải chi tiết:

a) Hai sóng cùng pha.

Giá trị cực đại của biên độ tổng hợp: A _max = 0,3 m Giá trị cực tiểu của biên độ tổng hợp: A _min = 0.

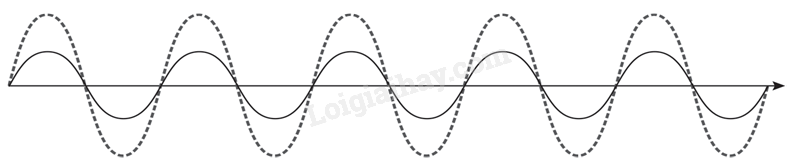b) Hai sóng lệch pha nhau 90 ^o .

Giá trị cực đại của biên độ tổng hợp: A _max = 0,2 m Giá trị cực tiểu của biên độ tổng hợp: A _min = 0,1 m.

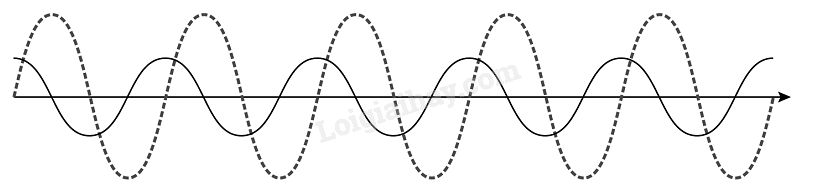
Giao thoa sóng 2.26

Trên mặt thoáng của chất lỏng có hai nguồn sóng A, B cách nhau 18 cm, dao động cùng pha theo phương thẳng đứng với tần số f = 10 Hz. Tốc độ truyền sóng trên mặt chất lỏng là 50 cm/s. a) Ta có thể quan sát thấy bao nhiêu điểm dao động với biên độ cực đại trên đoạn AB ? b) Số điểm dao động với biên độ cực đại trên đoạn AB cũng là số vân cực đại trong vùng giao thoa sóng của hai nguồn. Xác định số vân cực tiểu trong vùng giao thoa sóng của hai nguồn trên.

Phương pháp giải:

Vận dụng kiến thức đã học về biên độ dao động tại điểm M của hai sóng cùng pha:

- A _{Mm ax} = 2 A khi d ₂ – d ₁ = k λ \(\left( {k \in Z} \right)\)

- A _Mmin = 0 khi \({d_2}--{\rm{ }}{d_1} = \left( {k + \frac{1}{2}} \right)\lambda {\rm{ }}\left( {k \in Z} \right)\)

- Số điểm dao động với biên độ cực đại trên đoạn L : \( - L{\rm{ }} < k\lambda  < {\rm{ }}L\)

- Số điểm dao động với biên độ cực tiểu trên đoạn L : \( - L < \left( {k + \frac{1}{2}} \right)\lambda  < L\)

Lời giải chi tiết:

a) Bước sóng trên mặt chất lỏng là \(\lambda  = \frac{v}{f} = \frac{{50}}{{10}} = 5{\rm{ cm}}\)

Vì hai nguồn sóng A, B dao động cùng pha nên những điểm dao động với biên độ cực đại là những điểm có \({x_2}--{\rm{ }}{x_1} = k\lambda \)\(\left( {k \in Z} \right)\)

Số điểm dao động với biên độ cực đại trên đoạn AB là:

\(\begin{array}{*{20}{l}}{ - 18{\rm{ }} < k\lambda  < {\rm{ }}18}\\{ \Rightarrow  - 18{\rm{ }} < {\rm{ }}5k < {\rm{ }}18}\\{ \Rightarrow {\rm{ }} - 3,6{\rm{ }} < k < {\rm{ }}3,6}\\{ \Rightarrow k{\rm{ }} =  \pm 3;{\rm{ }} \pm {\rm{2}};{\rm{ }} \pm {\rm{1; 0}}}\end{array}\)

Ta có thể quan sát thấy 7 điểm dao động với biên độ cực đại trên đoạn AB .

b) Vì hai nguồn sóng A, B dao động cùng pha nên những điểm dao động với biên độ cực tiểu là những điểm có \({x_2}--{\rm{ }}{x_1} = \left( {k + \frac{1}{2}} \right)\lambda \)\(\left( {k \in Z} \right)\)

Số điểm dao động cực tiểu của hai nguồn trên là:

\(\begin{array}{*{20}{l}}{ - 18{\rm{ }} < \left( {k + \frac{1}{2}} \right)\lambda  < {\rm{ }}18}\\{ \Rightarrow  - 18{\rm{ }} < {\rm{ 5}}\left( {k + \frac{1}{2}} \right) < {\rm{ }}18}\\\begin{array}{l} \Rightarrow {\rm{ }} - 3,6{\rm{ }} < k + \frac{1}{2} < {\rm{ }}3,6\\ \Rightarrow {\rm{ }} - 4,1{\rm{ }} < k < {\rm{ }}3,1\end{array}\\{ \Rightarrow k{\rm{ }} =  - 4;{\rm{ }} \pm 3;{\rm{ }} \pm {\rm{2}};{\rm{ }} \pm {\rm{1; 0}}}\end{array}\)

Vậy hai nguồn trên có 8 điểm dao động cực tiểu.

Giao thoa sóng 2.27

Trong thí nghiệm giao thoa ánh sáng, hai khe Young được bố trí cách nhau a = 1,0 mm và khoảng cách từ hai khe đến màn quan sát là D = 4,8 m. Một đầu cảm biến ánh sáng được đặt tại vị trí của một vân tối trong hệ vân giao thoa. a) Khi sử dụng ánh sáng có bước sóng λ = 6,3.10 ^–7 m thì dịch đầu cảm biến đi một đoạn ngắn nhất là bao nhiêu thì cảm biến lại nhận giá trị nhỏ nhất? b) Kết quả thu nhận của cảm biến sẽ thay đổi như thế nào nếu giữ nguyên vị trí nhưng che đi một trong hai khe sáng?

Phương pháp giải:

Vận dụng kiến thức đã học về thí nghiệm về giao thoa ánh sáng với hai khe sáng hẹp của Young, các vân sáng, vân tối nằm xen kẽ và cách đều nhau trên màn quan sát. Khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp được gọi là khoảng vân và tính bằng công thức: \(i = \frac{{\lambda D}}{a}\)

Lời giải chi tiết:

a) Khoảng dịch của đầu cảm biến bằng khoảng cách giữa hai vân tối gần nhất, hay chính là khoảng vân:

\(i = \frac{{\lambda D}}{a} = \frac{{0,63.4,8}}{1} = 3{\rm{ mm}}\) b) Che một trong hai khe sáng thì mỗi điểm trên màn chỉ nhận được một sóng ánh sáng nên không xảy ra hiện tượng giao thoa. Tại vị trí đầu, cảm biến sẽ nhận được cường độ sáng lớn hơn.

Giao thoa sóng 2.28

Ánh sáng màu vàng có bước sóng 589 nm được dùng trong thí nghiệm hai khe Young. Khoảng cách hai khe là 0,20 mm và màn đặt cách hai khe 1,20 m. a) Tính khoảng vân của hệ vân giao thoa tạo thành trên màn. b) Trên vùng quan sát vân giao thoa rộng L = 46,0 mm sẽ quan sát được bao nhiêu vân sáng, vân tối?

Phương pháp giải:

Vận dụng kiến thức đã học về thí nghiệm về giao thoa ánh sáng với hai khe sáng hẹp của Young, các vân sáng, vân tối nằm xen kẽ và cách đều nhau trên màn quan sát. Khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp được gọi là khoảng vân và tính bằng công thức: \(i = \frac{{\lambda D}}{a}\)

- Số vân sáng trên đoạn L : \( - L{\rm{ }} < ki < {\rm{ }}L\)

- Số vân tối trên đoạn L : \( - L < \left( {k + \frac{1}{2}} \right)i < L\)

Lời giải chi tiết:

a) Khoảng vân trên màn là :

\(i = \frac{{\lambda D}}{a} = \frac{{0,589.1,2}}{{0,2}} = 3,5{\rm{ mm}}\) b)

\(\begin{array}{l} - 23 < ki < 23\\ \Rightarrow  - 23 < 3,5k < 23\\ \Leftrightarrow  - 6,6 < k < 6,6\\ \Rightarrow k = 0; \pm 1; \pm 2; \pm 3; \pm 4; \pm 5; \pm 6\end{array}\)

Trên màn quan sát được 13 vân sáng.

\(\begin{array}{l} - 23 < \left( {k + \frac{1}{2}} \right)i < 23\\ \Rightarrow  - 23 < 3,5\left( {k + \frac{1}{2}} \right) < 23\\ \Leftrightarrow  - 6,6 - \frac{1}{2} < k < 6,6 - \frac{1}{2}\\ \Leftrightarrow  - 7,1 < k < 6,1\\ \Rightarrow k = 0; - 7; \pm 1; \pm 2; \pm 3; \pm 4; \pm 5; \pm 6\end{array}\)

Trên màn quan sát được 14 vân sáng.

Giao thoa sóng 2.29

Một thí nghiệm giao thoa ánh sáng với hai khe Young có khoảng cách giữa hai khe 2,0 mm. Khoảng cách từ hai khe đến màn quan sát là 1,2 m. Hai khe được chiếu sáng đồng thời bởi hai ánh sáng có bước sóng λ ₁ = 500 nm và λ ₂ = 600 nm. Vân sáng chính giữa quan sát được trên màn là vị trí hai vân sáng của hai bức xạ trùng nhau. Hãy xác định khoảng cách từ vân chính giữa đến vân gần nhất cùng màu với vân chính giữa.

Phương pháp giải:

Vận dụng kiến thức đã học về giao thoa hai khe Young với hai ánh sáng đơn sắc khác nhau:

- Giao thoa ánh sáng với hai khe sáng hẹp của Young, các vân sáng, vân tối nằm xen kẽ và cách đều nhau trên màn quan sát. Khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp với cùng một bước sóng được gọi là khoảng vân và tính bằng công thức: \(i = \frac{{\lambda D}}{a}\)

- Tại vị trí hai vân của hai bước sóng trùng nhau: \(x = {k_1}\frac{{{\lambda _1}D}}{a} = {k_2}\frac{{{\lambda _2}D}}{a} \Rightarrow {k_1}{\lambda _1} = {k_2}{\lambda _2}{\rm{ }}\left( {{k_1},{k_2} \in Z} \right)\)

Lời giải chi tiết:

Vân chính giữa là vân sáng của hai bức xạ trùng nhau.

=> Vân cùng màu với vân chính giữa là vân sáng của hai bức xạ trùng nhau.

Chọn k ₁ , k ₂ nguyên dương.

Tại vị trí đó, ta có: \(\)\(\begin{array}{l}{x_1} = {x_2}\\ \Rightarrow {k_1}\frac{{{\lambda _1}D}}{a} = {k_2}\frac{{{\lambda _2}D}}{a}\\ \Rightarrow \frac{{{k_1}}}{{{k_2}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}} = \frac{{600}}{{500}} = \frac{6}{5}\end{array}\)

=> Vân gần nhất và cùng màu với vân chính giữa ứng với k ₁ = 6 ; k ₂ = 5.

\( \Rightarrow x = {k_1}\frac{{{\lambda _1}D}}{a} = 6.\frac{{0,5.1,2}}{2} = 1,8{\rm{ mm}}\)

Sóng dừng 2.30

Một sợi dây được căng theo phương thẳng đứng với hai đầu cố định. Thực hiện kích thích để trên dây có sóng dừng. Phát biểu nào dưới đây là đúng? A. Có thời điểm sợi dây duỗi thẳng. B. Hai điểm trên dây đối xứng nhau qua một nút sóng thì luôn dao động cùng pha nhau. C. Hai điểm trên dây đối xứng nhau qua một nút sóng thì luôn dao động ngược pha nhau. D. Khi giữ nguyên các điều kiện khác nhưng thả cho đầu dưới của dây tự do thì vẫn có sóng dừng ổn định trên dây.

Phương pháp giải:

Vận dụng kiến thức đã học về sóng dừng:

- Hiện tượng xuất hiện các điểm đứng yên ở những vị trí xác định khi đang có sóng lan truyền được gọi là hiện tượng sóng dừng. - Những điểm đứng yên gọi là nút sóng. Chính giữa hai nút sóng liên tiếp là bụng sóng.

- Khoảng cách giữa bụng sóng và nút sóng gần nhất:\(\frac{\lambda }{4}\).

- Khoảng cách giữa 2 nút hoặc 2 bụng gần nhất:\(\frac{\lambda }{2}\).

Lời giải chi tiết:

Đáp án: A. Có thời điểm sợi dây duỗi thẳng.

Sóng dừng 2.31

Một sợi dây AB đàn hồi được kéo căng và gắn cố định hai đầu. Đánh dấu điểm C chính giữa của sợi dây và hai điểm M, N đối xứng với nhau qua C . Khi trên dây quan sát được sóng dừng gồm ba nút là hai đầu A, B và điểm C thì dao động tại các điểm M và N sẽ: A. có biên độ như nhau và cùng pha. B. có biên độ khác nhau và cùng pha. C. có biên độ như nhau và ngược pha. D. có biên độ khác nhau và ngược pha.

Phương pháp giải:

Vận dụng kiến thức đã học về sóng dừng với hai đầu cố định: \(L = k\frac{\lambda }{2}{\rm{ }}\left( {k \in {N^*}} \right)\)

- Số bụng sóng = số bó sóng = k

- Số nút sóng = k + 1.

- Khoảng cách giữa bụng sóng và nút sóng gần nhất:\(\frac{\lambda }{4}\).

- Khoảng cách giữa 2 nút hoặc 2 bụng gần nhất:\(\frac{\lambda }{2}\).

Lời giải chi tiết:

Đáp án: C. có biên độ như nhau và ngược pha.

Sóng dừng 2.32

Để có sóng dừng trong ống cộng hưởng của âm với tần số f mà tại miệng ống tương ứng với vị trí nút sóng thì chiều dài L của ống (với k = 1, 2, 3…) là:

A. \(L = k\frac{v}{{2f}}.\)

B. \(L = k\frac{v}{f}.\)

C. \(L = \frac{v}{{kf}}.\)

D. \(L = 2\frac{v}{f}.\)

Phương pháp giải:

Vận dụng kiến thức đã học về sóng:

- Sóng dừng với hai đầu cố định: \(L = k\frac{\lambda }{2}{\rm{ }}\left( {k \in {N^*}} \right)\)

- Bước sóng λ là quãng đường mà sóng truyền đi trong một chu kì sóng: \(\lambda  = \frac{v}{f}\)

Lời giải chi tiết:

Đáp án: A. \(L = k\frac{v}{{2f}}.\)

Sóng dừng 2.33

Khi khảo sát hiện tượng sóng dừng trên một sợi dây căng giữa hai điểm cố định, người ta thay đổi tần số dao động kích thích cho dây. Kết quả ghi nhận được hai giá trị tần số gần nhau nhất cùng cho quan sát được sóng dừng trên dây là 525 Hz và 600 Hz. Giá trị tần số nhỏ nhất có thể tạo ra sóng dừng trên dây này là :

A. 50 Hz.

B. 75 Hz.

C. 100 Hz.

D. 125 Hz.

Phương pháp giải:

Vận dụng kiến thức đã học về sóng:

- Sóng dừng với hai đầu cố định: \(L = k\frac{v}{{2f}}{\rm{ }}\left( {k \in {N^*}} \right)\)

- Tần số có thể tạo ra sóng dừng trên dây phù hợp điều kiện: \(\frac{{2L}}{v} = \frac{{{k_1}}}{{{f_1}}} = \frac{{{k_2}}}{{{f_2}}} = ... = \frac{{{k_n}}}{{{f_n}}}\)

Lời giải chi tiết:

\(\begin{array}{l}L = {k_1}\frac{v}{{2{f_1}}} = \left( {{k_1} + 1} \right)\frac{v}{{2{f_2}}}\\ \Rightarrow \frac{{2L}}{v} = \frac{{{k_1}}}{{{f_1}}} = \frac{{{k_1} + 1}}{{{f_2}}}\\ \Rightarrow \frac{{{k_1}}}{{525}} = \frac{{{k_1} + 1}}{{600}} \Rightarrow {k_1} = 7\\\frac{{2L}}{v} = \frac{{{k_1}}}{{{f_1}}} = \frac{7}{{525}}\\ \Rightarrow \frac{{{k_{\min }}}}{{{f_{\min }}}} = \frac{{2L}}{v} = \frac{7}{{525}} = \frac{1}{{{f_{\min }}}}\\ \Rightarrow {f_{\min }} = 75{\rm{ Hz}}\end{array}\)

Đáp án: B. 75 Hz.

Sóng dừng 2.34

Sóng dừng thiết lập trên một dây đàn hồi có các nút liên tiếp cách nhau 25,0 cm. Hãy xác định: a) Bước sóng của sóng truyền trên dây. b) Khoảng cách từ nút sóng đến bụng sóng gần nhất.

Phương pháp giải:

Vận dụng kiến thức đã học về sóng dừng:

- Khoảng cách giữa bụng sóng và nút sóng gần nhất:\(\frac{\lambda }{4}\).

- Khoảng cách giữa 2 nút hoặc 2 bụng gần nhất:\(\frac{\lambda }{2}\).

Lời giải chi tiết:

a) Bước sóng của sóng truyền trên dây là λ = 25.2 = 50 cm b) Khoảng cách từ nút sóng đến bụng sóng gần nhất là \(\frac{\lambda }{4} = \frac{{50}}{4} = 12,5{\rm{ cm}}\)

Sóng dừng 2.35

Khi khảo sát sóng dừng của một sóng âm có tần số 2 500 Hz thì thấy giữa hai nút sóng cách nhau 21 cm thì có ba vị trí bụng sóng. a) Xác định bước sóng của sóng âm này. b) Xác định tốc độ truyền âm tại vùng không gian đang thực hiện khảo sát này.

Phương pháp giải:

Vận dụng kiến thức đã học về sóng dừng với hai đầu cố định: \(L = k\frac{\lambda }{2}{\rm{ }}\left( {k \in {N^*}} \right)\)

- Số bụng sóng = số bó sóng = k

- Số nút sóng = k + 1.

- Khoảng cách giữa bụng sóng và nút sóng gần nhất:\(\frac{\lambda }{4}\).

- Khoảng cách giữa 2 nút hoặc 2 bụng gần nhất:\(\frac{\lambda }{2}\).

- Tốc độ sóng là tốc độ lan truyền năng lượng của sóng trong không gian và được xác định theo công thức: v = fλ.

Lời giải chi tiết:

a) Khoảng cách giữa hai nút sóng đó là \(\frac{{3\lambda }}{2} = 21{\rm{ cm}}\)

Bước sóng của sóng âm này là \(\lambda  = 21.\frac{2}{3}{\rm{ = 14 cm}}\)

b) Tốc độ truyền âm tại vùng không gian đang thực hiện khảo sát này là:

v = λf = 14.10 ^-2 .2500 = 350 m/s

Sóng dừng 2.36

Một bạn học sinh dự định dùng cần rung có tần số là 20,0 Hz để tạo sóng dừng trên một sợi dây đàn hồi dài 1,2 m hai đầu cố định. Biết tốc độ truyền sóng trên dây khi quan sát được sóng dừng là 4,0 m/s. Số bụng sóng trên dây mà học sinh này có thể quan sát được là bao nhiêu?

Phương pháp giải:

Vận dụng kiến thức đã học về sóng dừng với hai đầu cố định: \(L = k\frac{\lambda }{2}{\rm{ }}\left( {k \in {N^*}} \right)\)

- Số bụng sóng = số bó sóng = k

- Số nút sóng = k + 1.

- Tốc độ sóng là tốc độ lan truyền năng lượng của sóng trong không gian và được xác định theo công thức: v = fλ.

Lời giải chi tiết:

Bước sóng của sóng dừng này là \(\lambda  = \frac{v}{f}{\rm{ = }}\frac{4}{{20}}{\rm{ = 0,2 m}}\)

Ta có: \(L = k\frac{\lambda }{2}\)

Số bụng sóng trên dây là: \(k = \frac{{2L}}{\lambda } = \frac{{2.1,2}}{{0,2}} = 12\)

Sóng dừng 2.37

Âm do một dây đàn ghita dài 80,0 cm phát ra có tần số nhỏ nhất là bao nhiêu để có thể quan sát thấy sóng dừng trên dây? Biết tốc độ truyền sóng trên dây đàn là 4,0.10 ² m/s.

Phương pháp giải:

Vận dụng kiến thức đã học về sóng:

- Sóng dừng với hai đầu cố định: \(L = k\frac{v}{{2f}}{\rm{ }}\left( {k \in {N^*}} \right)\)

- Tần số có thể tạo ra sóng dừng trên dây phù hợp điều kiện: \(\frac{{2L}}{v} = \frac{{{k_1}}}{{{f_1}}} = \frac{{{k_2}}}{{{f_2}}} = ... = \frac{{{k_n}}}{{{f_n}}}\)

Lời giải chi tiết:

Ta có \(\lambda  = \frac{v}{f}\)

Mà trong sóng dừng được cố định hai đầu: \(L = k\frac{\lambda }{2}\)

\(\begin{array}{l} \Rightarrow L = k\frac{v}{{2f}}\\ \Rightarrow f = k\frac{v}{{2L}} = k.\frac{{400}}{{2.0,8}} = 250k\end{array}\)

Tần số nhỏ nhất để quan sát sóng dừng trên dây đàn này là f = 250 Hz.

Sóng dừng 2.38

Một thí nghiệm khảo sát hiện tượng sóng dừng với sóng viba (loại sóng điện từ thường gặp ở lò vi sóng) được bố trí như Hình 2.6. Trong đó, đầu thu di chuyển từ từ trên một đường thẳng giữa máy phát sóng viba và màn phản xạ (được làm bằng kim loại) thì sẽ có những điểm thu được cường độ sóng cực đại và những điểm hầu như không ghi nhận có sóng.

a) Vẽ hình biểu diễn sóng dừng cho thí nghiệm này. Chỉ rõ tại màn phản xạ là nút hay bụng sóng. b) Trong thí nghiệm này, khoảng cách giữa hai vị trí liên tiếp mà đầu thu ghi nhận được cường độ sóng cực đại là 14 mm. Xác định bước sóng và tần số của sóng viba này. c) Với phương án thí nghiệm này thì xác định vị trí ứng với nút sóng hay bụng sóng sẽ dễ hơn? Vì sao?

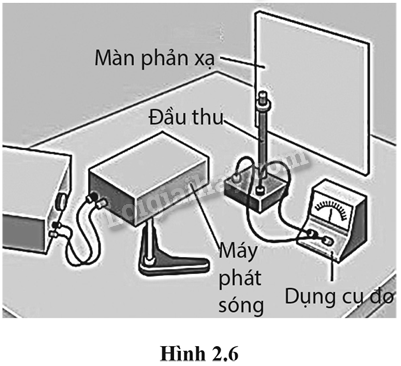
Phương pháp giải:

Vận dụng kiến thức đã học về sóng dừng:

- Hiện tượng xuất hiện các điểm đứng yên ở những vị trí xác định khi đang có sóng lan truyền được gọi là hiện tượng sóng dừng.

- Sóng dừng với hai đầu cố định: \(L = k\frac{\lambda }{2}{\rm{ }}\left( {k \in {N^*}} \right)\)

- Số bụng sóng = số bó sóng = k

- Số nút sóng = k + 1.

- Khoảng cách giữa bụng sóng và nút sóng gần nhất:\(\frac{\lambda }{4}\).

- Khoảng cách giữa 2 nút hoặc 2 bụng gần nhất:\(\frac{\lambda }{2}\).

Lời giải chi tiết:

a) Biểu diễn sóng dừng của sóng viba, vị trí màn phản xạ ứng với bụng sóng.

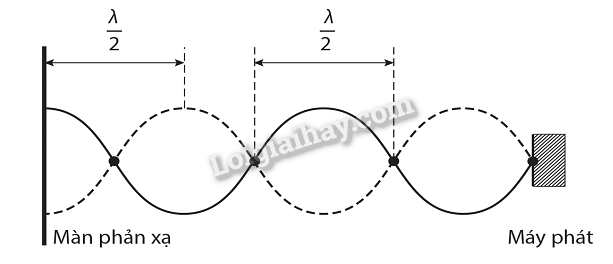
b) Khoảng cách giữa hai vị trí liên tiếp thu được cường độ sóng cực đại là khoảng cách giữa hai bụng sóng và bằng nửa bước sóng. Do đó, bước sóng của sóng này là 28 mm. Sóng viba truyền trong không khí với tốc độ c = 3,0.10 ⁸ m/s nên tần số của sóng trong thí nghiệm này là: \(f = \frac{c}{\lambda } = \frac{{{{3.10}^8}}}{{{{28.10}^{ - 3}}}} = 1,{1.10^{11}}{\rm{ Hz}}\)

c) Xác định vị trí nút sóng sẽ dễ hơn do cường độ sóng tại đó bằng 0.