Giải vật lí 10 bài 19 trang 120, 121, 122, 123, 124, 125 chân trời sáng tạo — Không quảng cáo

Câu hỏi tr 120 CH 1

Chứng minh công thức \(\overrightarrow F  = \frac{{\Delta \overrightarrow p }}{{\Delta t}}\) (19.1).

Phương pháp giải:

Vận dụng kiến thức đã học.

Biểu thức tính gia tốc: \(\overrightarrow a  = \frac{{\Delta \overrightarrow v }}{{\Delta t}}\)

Biểu thức tính độ biến thiên động lượng: \(\Delta \overrightarrow p  = m.\Delta \overrightarrow v \)

Lời giải chi tiết:

Xét một vật có khối lượng m không đổi trong suốt quá trình chuyển động. Khi vật chịu tác dụng bởi một lực không đổi \(\overrightarrow F \) thì gia tốc của vật là \(\overrightarrow a \)

Theo định luật II Newton, ta có:

\(\overrightarrow F  = m.\overrightarrow a  = m.\frac{{\Delta \overrightarrow v }}{{\Delta t}} = \frac{{\Delta \overrightarrow p }}{{\Delta t}}\)

=> đpcm

Câu hỏi tr 120 CH 2

Đưa ra phương án kéo một tờ giấy ra khỏi cốc nước (Hình 19.2) sao cho cốc nước không đổ. Giải thích và làm thí nghiệm kiểm chứng.

Phương pháp giải:

Biểu thức tính lực tác dụng lên một vật: \(\overrightarrow F  = \frac{{\Delta \overrightarrow p }}{{\Delta t}}\)

Lời giải chi tiết:

Để cốc nước không bị đổ thì vận tốc của tờ giấy phải đủ lớn và di chuyển ra khỏi càng nước càng nhanh, ít tác động đến cốc nước. Vì vậy cần phải tác động lên tờ giấy một lực thật mạnh

=> Phương án: Giật tờ giấy thật nhanh và dứt khoát, tay kéo tờ giấy xuống phía dưới và giật mạnh.

Học sinh tự làm thí nghiệm để kiểm chứng.

Câu hỏi tr 121 LT

Một trong những giải pháp khi cứu hộ người dân trong những vụ tai nạn hỏa hoạn ở nhà cao tầng là sử dụng đệm hơi. Đệm hơi được đặt ở vị trí thích hợp để người bị nạn có thể nhảy xuống an toàn (Hình 19.3). Thảo luận để trình bày vai trò của đệm hơi.

Phương pháp giải:

Vận dụng kiến thức đã học

Lời giải chi tiết:

Vai trò của đệm hơi:

- Đệm hấp thụ hoàn toàn động năng từ người tiếp đệm và không bị bật trở lại

- Đệm được lắp đặt nhanh chóng, dễ dàng bằng khí thổi liên tục, gọn gàng và thuận tiện khi vận chuyển.

Câu hỏi tr 121 CH 3

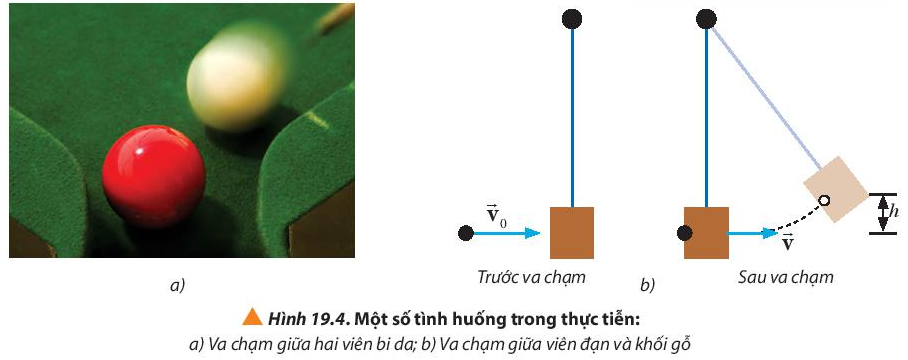
Quan sát Hình 19.4 mô tả về hai trường hợp va chạm và nhận xét những tính chất của va chạm:

a) Va chạm giữa hai viên bi da.

b) Va chạm giữa viên đạn và khối gỗ (viên đạn bị mắc lại trong khối gỗ sau khi va chạm).

Phương pháp giải:

Quan sát hình vẽ

Lời giải chi tiết:

a) Một viên bi da đang đứng yên, một viên khác đi tới và va chạm vào viên dang đứng yên, sau va chạm, hai viên chuyển động theo hai hướng khác nhau và khác với hướng ban đầu của viên bi da di chuyển.

=> Va chạm của hai viên bi da là va chạm đàn hồi (sau va chạm, vật lấy lại hình dạng ban đầu và tiếp tục chuyển động tách rời nhau).

b) Ban đầu miếng gỗ đang đứng yên, viên đạn bay tới, mắc vào miếng gỗ, sau va chạm hai vật chuyển động theo hướng ban đầu của viên đạn

=> Va chạm của viên đạn vào miếng gỗ là va chạm mềm ( sau va chạm, hai vật dính vào nhau và chuyển động theo chiều ban đầu).

Câu hỏi tr 122 CH 4

Lập luận để chứng tỏ tổng động lượng của hệ hai vật va chạm với nhau được bảo toàn.

Phương pháp giải:

Vận dụng kiến thức đã học

Lời giải chi tiết:

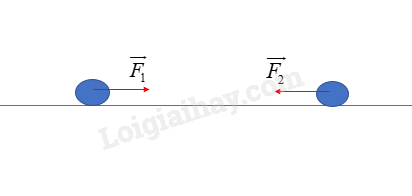
Xét một hệ cô lập gồm hai vật

Theo định luật III Newton, ta có: \(\overrightarrow {{F_1}}  =  - \overrightarrow {{F_2}} \)

Độ biến thiên động lượng: \(\Delta \overrightarrow {{p_1}}  = \overrightarrow {{F_1}} .\Delta t\); \(\Delta \overrightarrow {{p_2}}  = \overrightarrow {{F_2}} .\Delta t\)

Từ định luật III Newton ta có: \(\Delta \overrightarrow {{p_1}}  =  - \Delta \overrightarrow {{p_2}} \)

=> \(\Delta \overrightarrow {{p_1}}  + \Delta \overrightarrow {{p_2}}  = \overrightarrow 0  \Rightarrow \Delta \overrightarrow p  = \Delta \overrightarrow {{p_1}}  + \Delta \overrightarrow {{p_2}}  = \overrightarrow 0 \)

=> Độ biến thiên động lượng của hệ bằng 0, nghĩa là động lượng của hệ được không thay đổi, tức là được bảo toàn.

Câu hỏi tr 122 CH 5

Đề xuất phương án xác định tốc độ của hai xe ngay trước và sau va chạm với dụng cụ được gợi ý trong bài.

Phương pháp giải:

Vận dụng kiến thức đã học

Lời giải chi tiết:

Dụng cụ được gợi ý

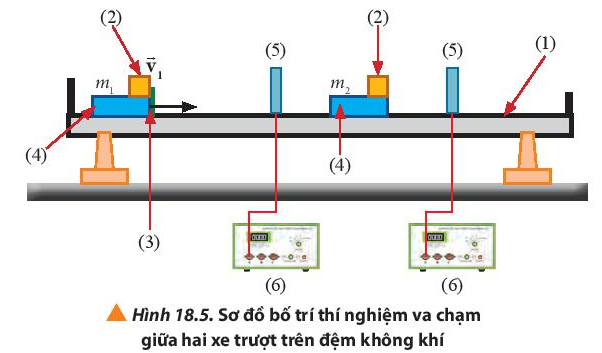
- Các bước xác định tốc độ của vật trước và sau va chạm

+ Bước 1: Gắn lò xo vào đầu của xe 1. Gắn 2 tấm chắn cổng quang điện lên mỗi xe.

+ Bước 2: Đo tổng khối lượng của xe 1 và xe 2 sau khi đã gắn lò xo và tấm chắn cổng quang điện

+ Bước 3: Giữ xe 2 đứng yên, đẩy cho xe 1 chuyển động đến va chạm với xe 2.

+ Bước 4: Đo thời gian hai xe đã đi qua cổng quang điện trước và sau va chạm

Chú ý: Tốc độ = Quãng đường / Thời gian.

Câu hỏi tr 122 CH 6

Khi xác định tốc độ của hai xe ngay trước và sau va chạm, em cần lưu ý gì đến dấu của vận tốc?

Phương pháp giải:

Vận dụng kiến thức đã học

Lời giải chi tiết:

Chọn chiều dương là chiều chuyển động của vật 1

Đối với va chạm đàn hồi, khi vật bật ngược trở lại thì vận tốc âm

Đối với va chạm mềm thì vận tốc của hệ vật mang dấu dương.

Câu hỏi tr 122 CH 7

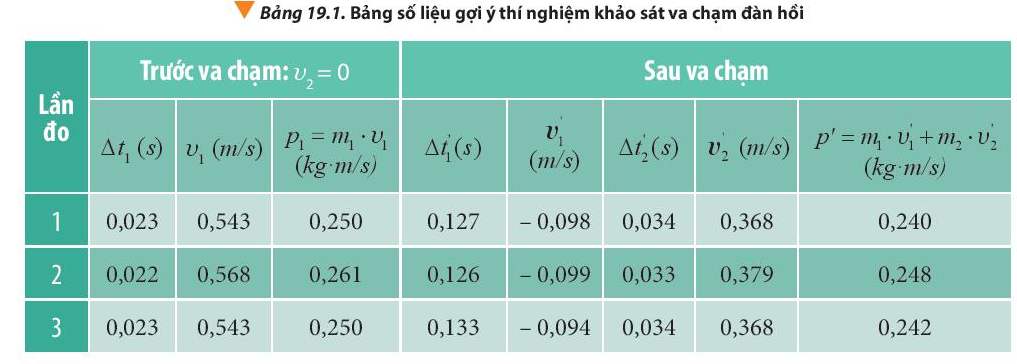
Dựa vào bảng số liệu ghi nhận được, tính toán động lượng của hai xe trước và sau va chạm.

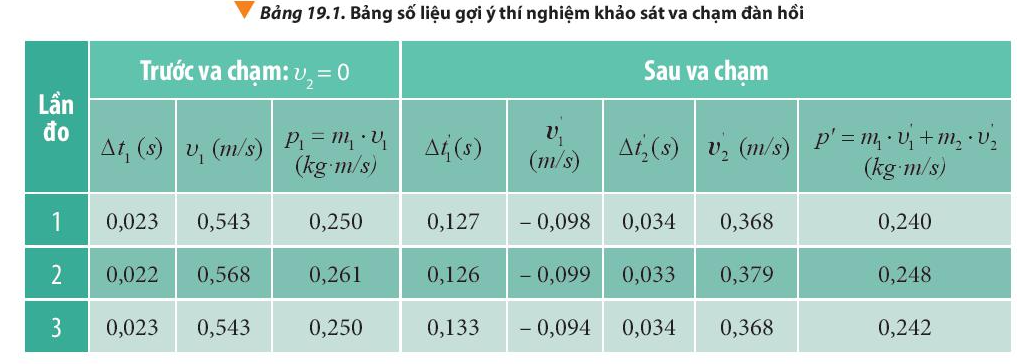
Phương pháp giải:

Quan sát bảng số liệu

Biểu thức tính động lượng trung bình: \(\overline p  = \frac{{{p_1} + {p_2} + ... + {p_n}}}{n}\)

Lời giải chi tiết:

Động lượng trước va chạm: \(\overline p  = \frac{{{p_1} + {p_2} + {p_3}}}{3} = \frac{{0,250 + 0,261 + 0,250}}{3} \approx 0,254(kg.m/s)\)

Động lượng của vật sau va chạm: \(\overline {{p'}}  = \frac{{p_1' + p_2' + p_3'}}{3} = \frac{{0,240 + 0,248 + 0,242}}{3} \approx 0,243(kg.m/s)\)

Câu hỏi tr 122 CH 8

Đánh giá sự thay đổi động lượng của từng xe và cả hệ trước và sau va chạm.

Phương pháp giải:

Biểu thức tính động lượng: p = m.v

Lời giải chi tiết:

- Lần đo 1:

+ \(\Delta {p_1} = \left| {{m_1}.({v_1} - v_1')} \right| = \left| {0,46.(0,543 - 0,098)} \right| = 0,2047(kg.m/s)\)

+\(\Delta {p_2} = \left| {{m_2}.({v_2} - v_2')} \right| = {m_2}.v_2' = 0,776.0,368 = 0,2856(kg.m/s)\)

- Lần đo 2:

+ \(\Delta {p_1} = \left| {{m_1}.({v_1} - v_1')} \right| = \left| {0,46.(0,568 - 0,099)} \right| = 0,2157(kg.m/s)\)

+ \(\Delta {p_2} = \left| {{m_2}.({v_2} - v_2')} \right| = {m_2}.v_2' = 0,776.0,379 = 0,2941(kg.m/s)\)

- Lần đo 3:

+ \(\Delta {p_1} = \left| {{m_1}.({v_1} - v_1')} \right| = \left| {0,46.(0,543 - 0,094)} \right| = 0,2065(kg.m/s)\)

+ \(\Delta {p_2} = \left| {{m_2}.({v_2} - v_2')} \right| = {m_2}.v_2' = 0,776.0,368 = 0,2856(kg.m/s)\)

=> Sau cả ba lần đo, sự thay đổi động lượng gần như nhau.

Câu hỏi tr 122 CH 9

Dựa vào kết quả đo vận tốc từ hai thí nghiệm trên, tiến hành tính toán và lập bảng số liệu về động năng của hai xe trước và sau va chạm (như gợi ý ở Bảng 19.2) cho cả hai loại va chạm.

Phương pháp giải:

Biểu thức tính động năng: \({W_d} = \frac{1}{2}m{v^2}\)

Lời giải chi tiết:

Bảng số liệu: m ₁ = 0, 46 kg; m ₂ = 0,776 kg

Va chạm mềm, học sinh tự thực hành để lấy số liệu, tính tương tự như va chạm đàn hồi.

Câu hỏi tr 122 CH 10

Đánh giá sự thay đổi năng lượng (thông qua động năng) của hệ trong hai va chạm đang xét.

Phương pháp giải:

Vận dụng kết quả câu 9

Lời giải chi tiết:

Từ bảng tính toán số liệu, ta thấy:

+ Va chạm đàn hồi: Động năng của hệ trước và sau va chạm gần bằng nhau.

+ Va chạm mềm: Động năng của hệ sau va chạm nhỏ hơn động năng của hệ trước va chạm.

Câu hỏi tr 123

Hãy kéo quả nặng đầu tiên của hệ con lắc Newton (Hình 19.5) lệch một góc nhỏ và thả ra. Quan sát, mô tả và giải thích hiện tượng.

Phương pháp giải:

Thực hiện thí nghiệm

Lời giải chi tiết:

Câu hỏi tr 124 CH 11

Ngoài việc bảo vệ cho đối phương, việc mang găng tay có bảo vệ gì cho bản thân võ sĩ hay không?

Phương pháp giải:

Vận dụng kiến thức đã học

Lời giải chi tiết:

+ Việc mang găng tay nhằm giảm thiểu chấn thương, trong đó có chấn thương não cho các võ sĩ

+ Ngoài ra, các võ sĩ thường có phản xạ dịch chuyển theo cú đấm của đối thủ khi bị tấn công nhằm giảm chấn thương cho bản thân mình.

Câu hỏi tr 124 CH 12

Phân tích ứng dụng kiến thức động lượng trong việc thiết kế đai an toàn và túi khí trong ô tô.

Phương pháp giải:

Vận dụng kiến thức đã học

Lời giải chi tiết:

Ứng dụng của đai an toàn và túi khí: giúp tăng thời gian va chạm của tài xế với các dụng cụ trong xe từ 10 đến 100 lần, điều này dẫn đến việc giảm đáng kể độ lớn của lực tác dụng lên tài xế và giảm thiểu khả năng chấn thương của tài xế.

Câu hỏi tr 124 LT

Quan sát Hình 19.10, dựa vào kiến thức động lượng để:

a) Giải thích tại sao một chú chim nhỏ lại có thể gây ra sự cố lớn cho máy bay như vết lõm ở Hình 19.10a trong sự cố ngày 30/9/2015 gần sân bay Nội Bài, Hà Nội.

b) Phân tích định tính cơ chế chuyển động của tên lửa (Hình 19.10b).

c) Giải thích tại sao bãi cát giúp giảm chấn thương cho vận động viên khi tiếp đất (19.10c).

Phương pháp giải:

Dựa vào kiến thức động lượng: Trong hệ kín, động lượng của hệ được bảo toàn

Lời giải chi tiết:

a) Tốc độ bay của máy bay rất lớn nên máy bay va chạm với chim trời trong thời gian rất ngắn, dẫn đến việc lực tác dụng giữa máy bay và chim rất lớn, vì vậy trên đầu máy bay có vết lõm lớn như vậy.

b) Cơ chế chuyển động của tên lửa: Khi nhiên liệu được đốt cháy trong buồng đốt, nó tạo ra áp suất lên thành buồng đốt cân bằng về mọi phía. ở vị trí ống phụt, áp suất bị giảm, vì thế áp suất ở phía đối diện sẽ đẩy tên lửa về phái trước.

c) Bãi cát giúp tăng lực ma sát, kéo dài thời gian vận động tiếp đất, từ đó làm giảm lực tiếp đất, giúp giảm chấn thương.

Câu hỏi tr 124 VD

Giả sử trong nhà em có em bé nhỏ, hãy đề xuất phương án xử lí nền nhà để hạn chế đến mức tối thiểu chấn thương khi em bé ngã. Giải thích tại sao chọn phương án đó.

Phương pháp giải:

Vận dụng kiến thức về động lượng

Lời giải chi tiết:

Để giảm tối thiểu chấn thương của em bé khi em bé ngã, ta nên để trên sàn nhà bằng những tấm thảm, vì vậy có thể làm giảm lực tiếp xúc của em bé với sàn nhà.

Câu hỏi tr 125 BT 1

Trong không trung, một con chim đại bàng nặng 1,8 kg bay đến bắt một con chim bồ câu nặng 0,65 kg đang bay cùng chiều với tốc độ 7 m/s. Biết tốc độ của chim đại bàng ngay trước khi bắt được bồ câu là 18 m/s (Hình 19P.1). Hãy tính tốc độ của chúng ngay sau khi đại bàng bắt được bồ câu.

Phương pháp giải:

Định luật bảo toàn động lượng:

\(\sum {\overrightarrow {{p_{tr}}}  = \sum {{{\overrightarrow p }_s}} } \)

Lời giải chi tiết:

Gọi:

+ Khối lượng, vận tốc trước và sau va chạm của chim đại bàng lần lượt là m ₁ , v ₁ , v’ ₁

+ Khối lượng, vận tốc trước và sau va chạm của chim bồ câu lần lượt là m ₂ , v ₂ , v’ ₂

Do va chạm của chim đại bàng và chim bồ câu là va chạm mềm nên ta có v’ ₁ = v’ ₂ = v’

Ta có: m ₁ = 1,8 kg; m ₂ = 0,65 kg; v ₁ = 18 m/s; v ₂ = 7 m/s

Chọn chiều dương là chiều chuyển động của chim đại bàng.

Áp dụng định luật bảo toàn động lượng, ta có:

\(\begin{array}{l}\sum {\overrightarrow {{p_{tr}}}  = \sum {{{\overrightarrow p }_s}} } \\ \Leftrightarrow {m_1}.\overrightarrow {{v_1}}  + {m_2}.\overrightarrow {{v_2}}  = ({m_1} + {m_2}).\overrightarrow {v'} \end{array}\)

Chiếu lên chiều dương, ta có:

\(\begin{array}{l}{m_1}.{v_1} + {m_2}.{v_2} = ({m_1} + {m_2}).v'\\ \Rightarrow v' = \frac{{{m_1}.{v_1} + {m_2}.{v_2}}}{{{m_1} + {m_2}}} = \frac{{1,8.18 + 0,65.7}}{{1,8 + 0,65}} \approx 15,08(m/s)\end{array}\)

Vậy tốc độ của chúng ngay sau khi chim đại bàng bắt được bồ câu là 15,08 m/s.

Câu hỏi tr 125 BT 2

Một võ sĩ Karate có thể dùng tay để chặt gãy một tấm gỗ như Hình 19P.2. Hãy xác định lực trung bình của tay tác dụng lên tấm gỗ. Lấy khối lượng của bàn tay và một phần cánh tay là 1 kg, tốc độ của cánh tay ngay trước khi chạm vào tấm gỗ là 10 m/s, thời gian tương tác là 2.10 ^-3 s.

Phương pháp giải:

Biểu thức tính động lượng: p = m.v

Biểu thức mối liên hệ giữa lực trung bình, động lượng, thời gian: \(\Delta p = F.\Delta t\)

Lời giải chi tiết:

Động lượng của cánh tay chạm vào khối gỗ là: p = m.v = 1.10 = 10 (kg.m/s)

Lực trung bình của tay tác dụng lên tấm gỗ là: \(F = \frac{{\Delta p}}{{\Delta t}} = \frac{{10}}{{{{2.10}^{ - 3}}}} = 5000(N)\)