Bài 2. Bảo toàn và chuyển hóa năng lượng trang 86, 87, 88, 89, 90, 91, 92, 93 Vật Lí 10 Cánh diều
Trong xây dựng, để có công trình bền vững thì cần xây nền móng chắc chắn bằng cách đóng những cọc bê tông đúc sẵn ngập sâu xuống nền đất. Tìm từ thích hợp với chỗ ? trong suy luận dưới đây: So sánh thế năng trọng trường của vật ở độ cao h với công của người tác dụng lực nâng vật lên đến độ cao này.
Câu hỏi tr 86
Trong xây dựng, để có công trình bền vững thì cần xây nền móng chắc chắn bằng cách đóng những cọc bê tông đúc sẵn ngập sâu xuống nền đất. Mỗi máy đóng cọc đều có bộ phận búa máy được nâng lên nhờ sức thủy lực, hơi nước hoặc động cơ điêzen. Khi đạt tới điểm cao nhất, búa máy sẽ được thả cho rơi xuống, va chạm mạnh vào cọc bê tông và làm nó lún xuống (hình 2.1). Như vậy, búa máy khi ở trên cao có dự trữ năng lượng (thế năng) để sinh công làm dịch chuyển cọc. Động năng mà búa máy truyền sang cọc có liên hệ gì với khối lượng của búa máy và độ cao của nó trước khi thả rơi?

Phương pháp giải:
Biểu thức tính động năng:
\({W_d} = \frac{1}{2}m{v^2}\)
Lời giải chi tiết:
Từ biểu thức tính động năng \({W_d} = \frac{1}{2}m{v^2}\), ta thấy động năng phụ thuộc vào khối lượng của vật và vận tốc, không phụ thuộc vào độ cao của vật trước khi thả rơi. Động năng tăng khi khối lượng của vật tăng.
Câu hỏi tr 87
- Tìm từ thích hợp với chỗ ? Trong suy luận dưới đây:
Thế năng của búa máy càng ? thì lực của máy đóng cọc thực hiện công càng ?, cọc lún xuống càng sâu.
- So sánh thế năng trọng trường của vật ở độ cao h với công của người tác dụng lực nâng vật lên đến độ cao này
Phương pháp giải:
Vận dụng lí thuyết đã học trong sách giáo khoa
Lời giải chi tiết:
- Thế năng của búa máy càng lớn thì lực của máy đóng cọc thực hiện công càng cao , cọc lún xuống càng sâu.
- Biểu thức tính thế năng trong trường trọng lực là: \({W_t} = m.g.h\)
Biểu thức tính công của trọng lực: A = m.g.h
=> W t = A
Câu hỏi tr 88 CH 1
Phan-Xi-Păng là ngọn núi cao nhất trong ba nước Việt nam, Lào, Campuchia, được mệnh danh là “nóc nhà Đông Dương”. Lên đến đỉnh núi cao 3147 m này ước mơ của nhiều bạn trẻ.
Tính thế năng của người leo núi có khối lượng 70 kg khi leo lên đến đỉnh núi Phan-Xi-Păng
Phương pháp giải:
Thế năng của vật ở độ cao h có độ lớn bằng công của lực dùng để nâng vật lên độ cao này
Lời giải chi tiết:
Công thực hiện của người leo núi là: A = m.g.h = 70.9,81.3147 = 2 161 045 (J)
=> Thế năng của người leo núi là: W t = 2 161 045 J.
Câu hỏi tr 88 CH 2
Từ liên hệ (i), (ii), hãy suy luận để rút ra kết luận: Động năng W đ của vật có giá trị bằng công A của lực tác dụng lên nó.
Liên hệ (i): v 2 = 2as
Liên hệ (ii): F = ma
Phương pháp giải:
Biểu thức tính động năng: \({W_d} = \frac{1}{2}m{v^2}\)
Lời giải chi tiết:
Từ liên hệ (ii) ta có: \(m = \frac{F}{a}\) (iii)
Thay (i) và (iii) vào biểu thức tính động năng ta có:
\({W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}.\frac{F}{a}.2as = F.s = A\)
Vậy động năng của vật có giá trị bằng công của lực tác dụng lên nó.
Câu hỏi tr 88 CH 3
So sánh động năng của ô tô nặng 1000 kg chuyển động với tốc độ 4 m/s và động năng của xe máy năng 100 kg chuyển động với tốc độ 15 m/s
Phương pháp giải:
Biểu thức tính động năng: \({W_d} = \frac{1}{2}m{v^2}\)
Trong đó:
+ m: khối lượng vật (kg)
+ v: tốc độ của vật (m/s)
Lời giải chi tiết:
Động năng của ô tô là: \({W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}{.1000.4^2} = 8000(J)\)
Động năng của xe máy là: \({W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}{.100.15^2} = 11250(J)\)
Câu hỏi tr 89 CH 1
- Năng lượng hao phí trong quá trình toa tàu chuyển động tồn tại dưới dạng nào?
- Bạn chà xát hai bàn tay vào nhau liên tục cho đến khi lòng bàn tay ấm lên. Năng lượng nhiệt mà bạn cảm nhận được chuyển hóa từ dạng năng lượng nào?
Phương pháp giải:
Vận dụng kiến thức đã học trong KHTN 6
Lời giải chi tiết:
- Năng lượng hao phí trong quá trình toa tàu chuyển động tồn tại dưới dạng nhiệt năng.
- Bạn chà xát hai bàn tay vào nhau liên tục cho đến khi lòng bàn tay ấm lên. Năng lượng nhiệt mà bạn cảm nhận được chuyển hóa từ động năng.
Câu hỏi tr 89 CH 2
Phân tích sự chuyển hóa động năng và thế năng của vật trong một số trường hợp đơn giản. Trong các trường hợp này có sự hao phí năng lượng không?
Bạn có thể sử dụng các trường hợp ở hình 2.4 hoặc tự đưa ra các tình huống khác.
Phương pháp giải:
Liên hệ thực tế và vận dụng kiến thức về năng lượng
Lời giải chi tiết:
Ví dụ: Ném một vật lên cao
Phân tích:
+ Khi ném vật lên trên cao, vận tốc của vật giảm dần dẫn đến động năng giảm dần, ngược lại độ cao tăng dần nên thế năng tăng dần. Khi lên đến độ cao cực đại thì thế năng cực đại và động năng bằng 0.
+ Sau đó, vật rơi xuống mặt đất, thế năng giảm dần và động năng tăng dần
+ Tiếp tục, vật lại nảy lên cao nhưng không cao bằng lần đầu tiên, sau đó lại hạ xuống mặt đất, cứ như vậy cho đến khi dừng hẳn
+ Vật lên cao thì thế năng tăng và động năng giảm, vật xuống thấp thì động năng tăng và thế năng giảm
+ Trong quá trình di chuyển của vật, ta thấy vật lên cao càng ngày càng thấp dần xuống do ngoài có sự chuyển hóa giữa thế năng và động năng thì còn có nhiệt năng được sinh ra.
Câu hỏi tr 90 CH 1
Cơ năng là gì?
Phương pháp giải:
Vận dụng kiến thức đã học trong sách giáo khoa
Lời giải chi tiết:
Cơ năng của một vật là tổng động năng và thế năng.
Câu hỏi tr 90 CH 2
Điều kiện để cơ năng của vật được bảo toàn là gì?
Phương pháp giải:
Vận dụng kiến thức đã học trong SGK
Lời giải chi tiết:
Điều kiện để cơ năng được bảo toàn là trong quá trình chuyển hóa không kèm theo sự hao phí năng lượng.
Câu hỏi tr 90 CH 3
Giải lại bài tập minh họa với m = 10 kg. Chứng minh rằng tốc độ lớn nhất của quả lắc không phụ thuộc vào khối lượng của nó.

Phương pháp giải:
Vận dụng kiến thức đã học
Lời giải chi tiết:
Thế năng của quả lắc so với vị trí thấp nhất trên quỹ đạo là: W t = m.g.h = 10.9,81.0,15 = 14,72 (J)
Ở vị trí thấp nhất trên quỹ đạo, toàn bộ thế năng của vật đã chuyển hóa thành động năng vì ma sát trong quá trình chuyển động là không đáng kể.
W đ = W t = 14, 72 J
Từ công thức động năng \({W_d} = \frac{1}{2}m{v^2}\), suy ra:
\(v = \sqrt {\frac{{2.{W_d}}}{m}} = \sqrt {\frac{{2.14,72}}{{10}}} \approx 1,72(m/s)\)
=> Tốc độ lớn nhất của quả lắc không phụ thuộc vào khối lượng của nó.
Câu hỏi tr 91 CH 1
Nhảy cầu là một môn thể thao. Vận động viên nhảy lên, đạt điểm cao nhất cách mặt nước 10 m, rồi rơi xuống. Trong quá trình rơi, vận động viên thực hiện các động tác nhào lộn đẹp mắt trước khi chạm nước (hình 2.6). Em hãy ước lượng tốc độ của vận động viên khi chạm nước. Nước trong bể có vai trò như thế nào trong việc đảm bảo an toàn cho vận động viên?
Phương pháp giải:
Vận tốc của vật trong rơi tự do: \(v = \sqrt {2gh} \)
Lời giải chi tiết:
Tốc độ của vận động viên khi chạm nước là: \(v = \sqrt {2gh} = \sqrt {2.9,81.10} \approx 14(m/s)\)
Nước trong bể có vài trò làm giảm tốc độ của vận động viên khi vận động viên tiếp nước.
Câu hỏi tr 91 CH 2
Một em bé có khối lượng 20 kg trượt từ đỉnh cầu trượt cao 2 m. Khi tới chân cầu trượt, em bé có tốc độ là 4 m/s. Cơ năng của em bé có bảo toàn không? Tại sao?
Phương pháp giải:
Biểu thức tính cơ năng: \(W = {W_d} + {W_t}\). Trong quá trình chuyển động, cơ năng có giá trị không thay đổi thì cơ năng được bảo toàn.
Biểu thức tính động năng: \({W_d} = \frac{1}{2}m{v^2}\)
Biểu thức tính thế năng: \({W_t} = mgh\)
Lời giải chi tiết:
Tại đỉnh cầu trượt, động năng bằng 0, thế năng là: \({W_t} = mgh = 20.9,81.2 = 392,4(J)\)
=> Cơ năng tại đỉnh cầu là: \(W = {W_d} + {W_t} = 0 + 392,4 = 392,4(J)\)
Tại chân cầu trượt, thế năng của em bé bằng 0, động năng là: \({W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}{.20.4^2} = 160(J)\)
=> Cơ năng tại chân cầu là: \(W = {W_d} + {W_t} = 160 + 0 = 160(J)\)
=> Cơ năng tại chân cầu khác cơ năng tại đỉnh cầu, vậy cơ năng của em bé không được bảo toàn.
Câu hỏi tr 91 CH 3
Lấy ví dụ về sự chuyển hóa từ năng lượng dự trữ thành năng lượng hoạt động trong cuộc sống và sản xuất nông nghiệp, công nghiệp.
Phương pháp giải:
Liên hệ thực tế
Lời giải chi tiết:
Trong cuộc sống: Uống một hộp sữa milo 180 ml chứa năng lượng 110 Kcal tương đương với 459 800 J
Trong sản xuất nông nghiệp, công nghiệp: Rắc phân bón, phân lân, kali cho cây trồng cung cấp năng lượng cho cây để cây phát triển.
Câu hỏi tr 92 CH 1
Máy tời đang hoạt động với công suất 1000 W đưa 100 kg vật liệu lên đều tới độ cao 16 m trong 20 s. Tính hiệu suất của máy tời.
Phương pháp giải:
Biểu thức tính hiệu suất: \(H = \frac{{{W_{có ích}}}}{{{W_{cung cấp}}}}.100\% \)
Trong đó:
+ W có ích là năng lượng có ích được tạo ra (J)
+ W cung cấp là năng lượng cung cấp (J)
Lời giải chi tiết:
Lấy g = 10 m/s 2
+ Năng lượng máy cung cấp là: W cung cấp = P.t = 1000.20 = 20 000 (J)
+ Năng lượng có ích là: W có ích = m.g.h = 100.10.16 = 16 000 (J)
=> Hiệu suất của máy tời là: \(H = \frac{{{W_{có ích}}}}{{{W_{cungcap}}}}.100\% = \frac{{16000}}{{20000}}.100\% = 80\% \)
Câu hỏi tr 92 CH 2
Với mỗi động cơ ở bảng 2.1, chỉ ra dạng năng lượng cung cấp, dạng năng lượng có ích tạo ra, dạng năng lượng hao phí tạo ra và biểu diễn dưới dạng lược đồ như hình 2.7.

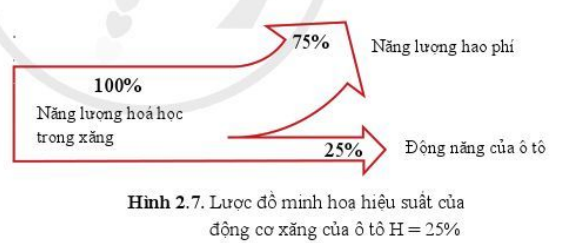
Phương pháp giải:
Quan sát hình
Lời giải chi tiết:
- Động cơ điện

- Động cơ hơi nước

- Động cơ ô tô:
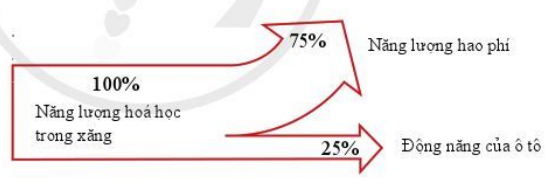
Câu hỏi tr 92 CH 3
Tại sao cần tắt điều hòa, tắt đài, tắt đèn trong ô tô khi ô tô đang đi trên đường mà gần hết xăng.
Phương pháp giải:
Vận dụng lí thuyết năng lượng
Lời giải chi tiết:
Ô tô sử dụng năng lượng để hoạt động là xăng. Trong ô tô, tất cả các thiết bị hoạt động được đều sử dụng năng lượng, nếu như ô tô sắp hết xăng thì năng lượng cũng gần như cạn kiệt, vì vậy nếu ô tô đang đi trên đường thì nên tắt điều hòa, tắt đài, tắt đèn để tất cả năng lượng xăng tập trung vào động cơ để xe hoạt động.
Câu hỏi tr 93
Chế tạo mô hình đơn giản và minh họa định luật bảo toàn năng lượng, liên quan đến một số dạng năng lượng khác nhau.
Phương pháp giải:
Vận dụng lí thuyết năng lượng
Lời giải chi tiết:
Mô hình đơn giản minh họa sự bảo toàn năng lượng
