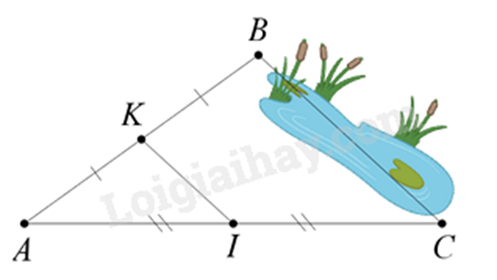
1. Giữa hai điểm \(B\) và \(C\) bị ngăn cách bởi hồ nước (như hình dưới). Hãy xác định độ dài \(BC\) mà không cần phải bơi qua hồ. Biết rằng đoạn thẳng \(KI\) dài \(30m\) và \(K\) là trung điểm của \(AB\), \(I\) là trung điểm của \(AC\).
2. Cho tam giác \(ABC\) vuông tại \(A\), đường trung tuyến \(AM\). Gọi \(H\) là điểm đối xứng với \(M\) qua \(AB\), \(E\) là giao điểm của \(MH\) và \(AB\). Gọi \(K\) là điểm đối xứng với \(M\) qua \(AC\), \(F\) là giao điểm của \(MK\) và \(AC\).
a) Các tứ giác \(AEMF\), \(AMBH\), \(AMCK\) là hình gì? Vì sao?
b) Chứng minh rằng \(H\) đối xứng với \(K\) qua \(A\).
c) Tam giác vuông \(ABC\) cần thêm điều kiện gì thì tứ giác \(AEMF\) là hình vuông?
- Dựa vào tính chất đường trung bình trong tam giác.
a) Tứ giác \(AEMF\) là hình chữ nhật. Các tứ giác \(AMBH\), \(AMCK\) là hình thoi.
b) Theo a) suy ra \(HA\parallel BC\), \(AK\parallel MC\) \( \Rightarrow \) \(H\), \(A\), \(K\) thẳng hàng. Lại có \(AH = AM = AK\) \( \Rightarrow \) \(H\), \(K\) đối xứng với nhau qua \(A\).
c) Để hình chữ nhật \(AEMF\) là hình vuông thì cần thêm điều kiện \(AE = EM\). \( \Rightarrow \) \(AB = AC\). Vậy tam giác \(ABC\) vuông cân tại \(A\).
1.
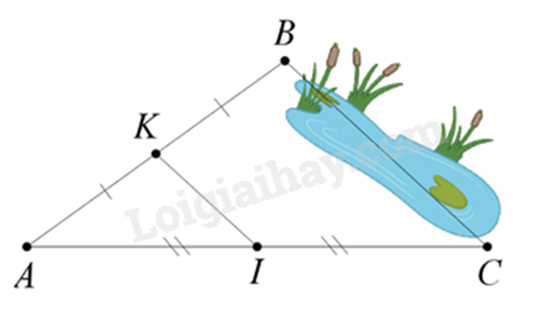
Vì K là trung điểm của AB, I là trung điểm của AC nên KI là đường trung bình của tam giác ABC => KI // BC và KI = \(\frac{1}{2}\)BC.
Vì KI = 30 m nên BC = 2.KI = 2.30 = 60 m.
Vậy BC = 60 m.
2.
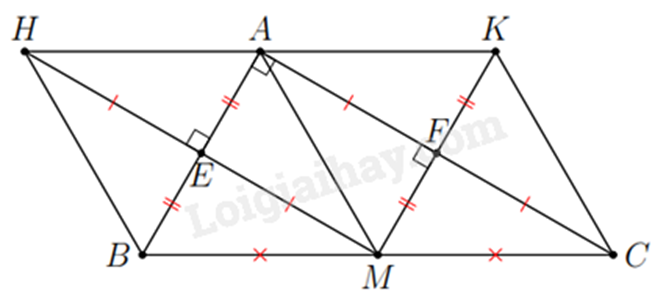
a) Ta có: \(H\) là điểm đối xứng với \(M\) qua \(AB\), \(E\) là giao điểm của \(MH\) và \(AB\) => \(AB \bot HM\)(\(\widehat E = {90^0}\)) và HE = EM.
\(K\) là điểm đối xứng với \(M\) qua \(AC\), \(F\) là giao điểm của \(MK\) và \(AC\)=> \(AC \bot MK\)(\(\widehat F = {90^0}\)) và MF = FK.
Tứ giác AEMF có: \(\widehat A = \widehat E = \widehat F = {90^0}\) (cmt) nên AEMF là hình chữ nhật (đpcm). Suy ra ME // AF; MF // AE.
Ta có: M là trung điểm của BC (vì AM là đường trung tuyến), ME // AC (cmt); MF // AE (cmt) => ME và MF là đường trung bình của tam giác ABC. => ME = \(\frac{1}{2}\)AC; MF = \(\frac{1}{2}\)AB. (1)
Mà ME = AF; MF = AE (vì AEMF là hình chữ nhật) (2)
Từ (1) và (2) suy ra AE = EB = \(\frac{1}{2}\)AB; AF = FC = \(\frac{1}{2}\)AC.
Xét tứ giác AMBH có: AE = EB; HE = EM và \(AB \bot HM\) tại E nên AMBH là hình thoi (đpcm).
Tương tự, tứ giác AMCK có: AF = FC; MF = FK và \(AC \bot MK\) tại F nên AMCK là hình thoi (đpcm).
b) Xét tứ giác BHKC có: BH // CK và BH = CK (cùng song song và bằng AM) nên BHKC là hình bình hành => BC // HK.
Vì AMBH và AMCK là hình thoi nên HA // BM, HA = BM; AK // CM, AK = CM.
Ta có BC // HK, BC // HA; BC // AK (cmt) => H, A, K thẳng hàng.
Mà AH = AK = BM = MC (vì M là trung điểm của BC) nên H đối xứng với K qua A.
c) Để AEMF là hình vuông thì AE = AF \( \Leftrightarrow \) \(\frac{1}{2}AB = \frac{1}{2}AC\) hay AB = AC \( \Leftrightarrow \) tam giác ABC vuông cân tại A.
Vậy để AEMF là hình vuông thì tam giác ABC phải là tam giác cân.