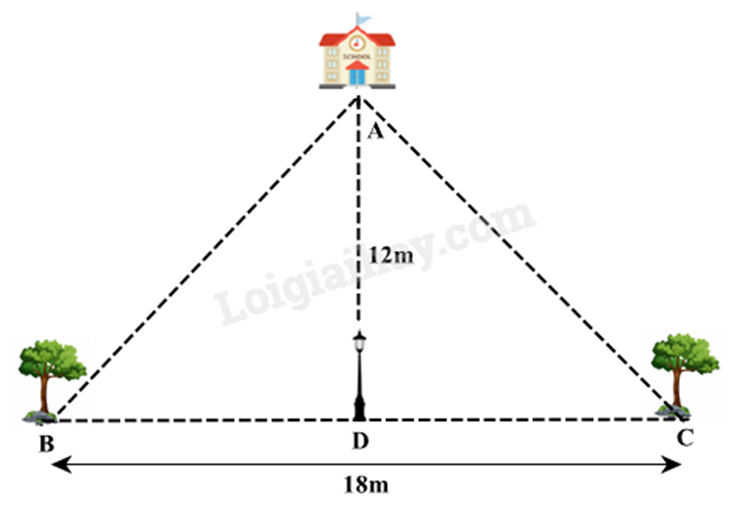
Hai cây B và C được trồng dọc trên đường, cách nhau 18m và — Không quảng cáo

Phương pháp giải

Chứng minh $\Delta ABD = \Delta ACD$ suy ra AB = AC.

Áp dụng định lí Pythagore để tính khoảng cách.

Vì hai cây B và C được trồng cách đều cột đèn D nên BD = CD = $\frac{1}{2}$BC = $\frac{1}{2}$.18 = 9(m)

Vì ngôi trường A cách cột đèn D 12m theo hướng vuông góc nên $\widehat {ADC} = {90^o}$.

Xét $\Delta ABD$ và $\Delta ACD$ có:

$AD$ chung

$\widehat {ADB} = \widehat {ADC} = \left( {{{90}^0}} \right)$

BD = DC (cmt)

$\Rightarrow \Delta ABD = \Delta ACD$ (hai cạnh góc vuông)

$\Rightarrow AB = AC$

Áp dụng định lí Pythagore vào tam giác vuông ADC, ta có:

$\begin{array}{l}A{C^2} = A{D^2} + D{C^2} = {12^2} + {9^2} = 225\\ \Rightarrow AC = \sqrt {225}  = 15\left( m \right)\end{array}$

Vậy khoảng cách từ mỗi cây đến ngôi trường là 15m.