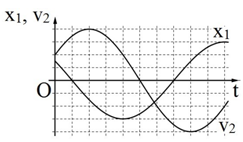
Hai vật M 1 và M 2 dao động điều hòa cùng tần số. Hình bên là đồ thị biểu diễn sự phụ thuộc của li độ x 1 của M 1 và vận tốc v 2 của M 2 theo thời gian t . Hai dao động của M 2 và M 1 lệch pha nhau:
-
A.
\(\frac{{5\pi }}{6}\)
-
B.
\(\frac{\pi }{6}\)
-
C.
\(\frac{{2\pi }}{3}\)
-
D.
\(\frac{\pi }{3}\)
Tìm pha ban đầu của x 1 ; v 2 , từ đó tìm pha ban đầu của x 2 . Sau đó tìm hiệu số pha.
Gọi mỗi 1 ô trong đồ thị là 1 đơn vị, ta có T = 12.
Với x 1 thì sau thời gian t = 1 thì x 1 = 0 lần đầu tiên (giá trị x đang giảm), vậy góc mà vecto quay OM 1 quét được là:
\(\Delta {\varphi _1} = \frac{1}{{12}}.2\pi = \frac{\pi }{6}rad\)
Suy ra pha ban đầu của x 1 là :
\({\varphi _1} = \frac{\pi }{2} - \frac{\pi }{6} = \frac{\pi }{3}rad\)
Với v 2 thì ban đầu v 02 bằng nửa giá trị cực đại và đang tăng nên ta có :
\({{\rm{W}}_{d20}} = \frac{1}{4}{\rm{W}} \Rightarrow {{\rm{W}}_t} = \frac{3}{4}{\rm{W}} \Rightarrow x = \pm \frac{{\sqrt 3 }}{2}A\)
Vì vận tốc đang tăng nên thế năng đang giảm, nên ta Đáp án :
\({x_{20}} = \frac{{\sqrt 3 }}{2}A\)
Ta có giản đồ vectơ
Khi đó vecto quay OM 2 ở vị trí như trên hình:

Suy ra pha ban đầu của x 2 là:
\({\varphi _2} = \frac{\pi }{6}\)
Độ lệch pha của x 1 với x 2 là:
Đáp án B.
Đáp án : B