1. Hình ảnh bên dưới là một thiết kế ngôi nhà hình tam giác cân đang là xu thế mới trên khắp thế giới ở phân khúc nhà nhỏ. Đây là những thiết kế cơ động, có thể thi công lắp dựng nhanh có chi phí rẻ. Trước ngôi nhà có lắp một tấm kính chống vỡ có dạng tam giác cân . Biết cạnh đáy, cạnh bên của miếng kính này lần lượt có độ dài là 8m và 10m. Tính chiều cao của tấm kính tam giác cân này (làm tròn kết quả đến hàng phần mười) ?

2. Cho hình thang ABCD có độ dài đáy lớn bằng 2 lần đáy nhỏ CD . Gọi I là trung điểm của AB . Đường thẳng AD cắt đường thẳng BC tại E . a) Chứng minh: tứ giác AICD và tứ giác BCDI là hình bình hành.
b) Chứng minh: \(\widehat {DIA} = \widehat {ECD}\) và AD = DE.
c) Giả sử \(\widehat A = \widehat D = {90^0}\)và AD = CD. Chứng minh \(BC \bot AC\).
1. Dựa vào định lí Pythagore để tính chiều cao của tấm kính.
2.
a) Chứng minh tứ giác AICD; BCDI có cặp cạnh đối song song và bằng nhau nên là hình bình hành.
b) Dựa vào tính chất hai đường thẳng song song để chứng minh \(\widehat {DIA} = \widehat {ECD}\).
Dựa vào tính chất hình bình hành để chứng minh AD = DE.
c) \(\widehat A = \widehat D = {90^0}\) và AD = CD nên hình bình hành AICD trở thành hình vuông. Sử dụng tính chất của hình vuông và hai đường thẳng song song để chứng minh \(BC \bot AC\).
1.
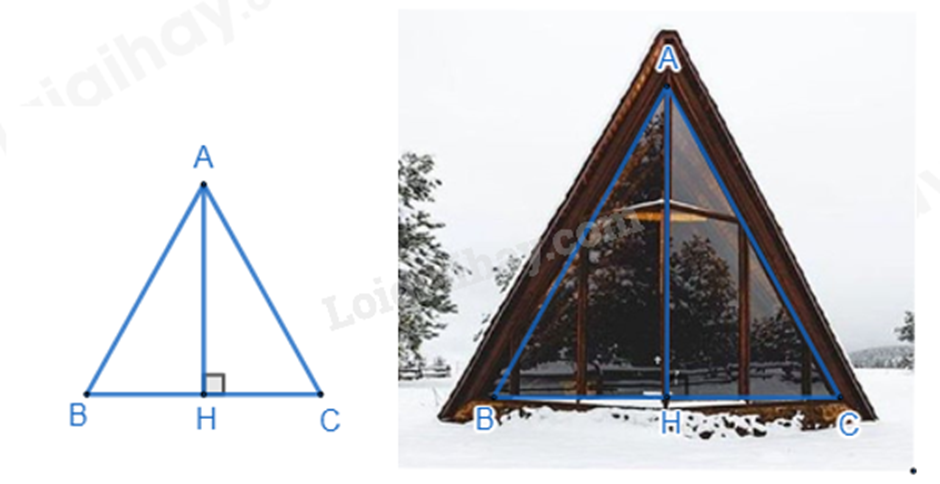
Gọi tam giác ABC là tam giác biểu thị tấm kính tam giác cân.
Kẻ \(AH \bot BC\) (H \( \in \) BC). Vì tam giác ABC cân tại A nên AH vừa là đường cao vừa là đường trung tuyến của tam giác ABC. Khi đó H là trung điểm của BC suy ra \(BH = \frac{1}{2}BC = \frac{1}{2}.8 = 4(m)\).
Áp dụng định lí Pythagore vào tam giác vuông AHB, ta có:
\(\begin{array}{l}A{H^2} = A{B^2} - B{H^2} = {10^2} - {4^2} = 84\\AH = \sqrt {84} \approx 9,2(m)\end{array}\)
Vậy chiều cao của tấm kính tam giác cân này xấp xỉ 9,2m.
2.
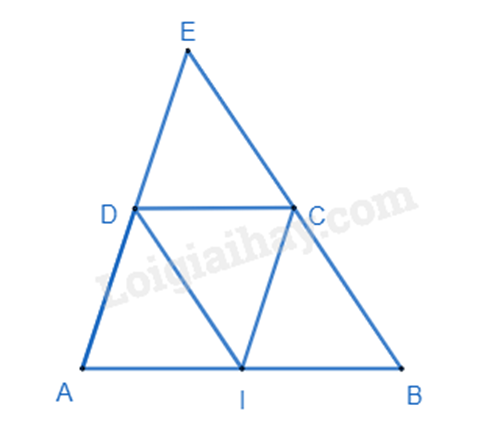
a) Ta có I là trung điểm của AB nên \(AI = IB = \frac{1}{2}AB\). Mà CD = \(\frac{1}{2}\)AB suy ra AI = IB = CD.
Xét tứ giác AICD có:
AI // CD (I \( \in \) AB)
AI = CD (cmt)
=> AICD là hình bình hành. (đpcm)
Xét tứ giác BCDI có:
BI // CD (I \( \in \) AB)
BI = CD (cmt)
=> BCDI là hình bình hành. (đpcm)
b) BCDI là hình bình hành nên BC // DI => \(\widehat {DIA} = \widehat {CBI}\) (hai góc đồng vị).
BI // CD nên \(\widehat {CBI} = \widehat {ECD}\) (hai góc đồng vị).
=> \(\widehat {DIA} = \widehat {ECD}\) (đpcm).
AICD là hình bình hành nên CI // AD và CI = AD. (1)
Xét tứ giác CEDI có:
CI // DE (CI // AD)
DI // CE (DI // BC)
=> CEDI là hình bình hành => CI = DE (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra AD = DE. (đpcm)
c) Vì \(\widehat A = \widehat D = {90^0}\)và AD = CD nên hình bình hành AICD trở thành hình vuông. Khi đó AC \( \bot \) DI.
Mà DI // BC nên AC \( \bot \) BC. (đpcm)