Đề bài
Hình thang ABCD (AB // CD) có các tia phân giác của \(\widehat A{,^{}}\widehat D\) cắt nhau tại M thì
-
A.
\(\widehat {AM{{D}}} = {180^o}\)
-
B.
\(\widehat {AM{{D}}} = {150^o}\)
-
C.
\(\widehat {AM{{D}}} = {90^o}\)
-
D.
\(\widehat {AM{{D}}} = {60^o}\)
Phương pháp giải
Sử dụng tính chất của tia phân giác.
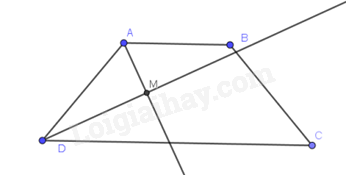
Hình thang ABCD (AB // CD) có các tia phân giác của \(\widehat A{,^{}}\widehat D\) cắt nhau tại M nên
\(\widehat {DAM} + \widehat {ADM} = \frac{1}{2}\left( {\widehat A + \widehat D} \right) = \frac{1}{2}{.180^o} = {90^o}\)
Vậy \(\widehat {AM{{D}}} = {90^o}\)
Đáp án : C