Kết quả kiểm tra môn Toán và Ngữ văn của một số học sinh được lựa chọn ngẫu nhiên cho ở bảng sau:
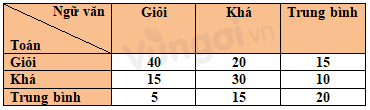
Ví dụ: Số học sinh có kết quả Toán – giỏi , Ngữ văn – giỏi là 40 . Minh họa

Hãy tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả:
Môn Toán đạt loại giỏi
-
A.
\(\dfrac{{15}}{{34}}\)
-
B.
\(\dfrac{4}{{17}}\)
-
C.
\(\dfrac{6}{{17}}\)
-
D.
\(\dfrac{{13}}{{34}}\)
Đáp án: A
- Tính tổng số học sinh được lựa chọn.
- Tính số học sinh được loại giỏi môn Toán.
- Xác suất thực nghiệm=Số học sinh được loại giỏi môn Toán:Tổng số học sinh được lựa chọn.
Tổng số học sinh là tổng tất cả các số trên bảng: 170.
Số học sinh được loại giỏi môn Toán là 40+20+15=75
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên được loại giỏi môn Toán là \(\dfrac{{75}}{{170}} = \dfrac{{15}}{{34}}\)
Loại khá trở lên ở cả hai môn
-
A.
\(\dfrac{9}{{17}}\)
-
B.
\(\dfrac{7}{{17}}\)
-
C.
\(\dfrac{{21}}{{34}}\)
-
D.
\(\dfrac{7}{{34}}\)
Đáp án: C
- Tính tổng số học sinh được lựa chọn.
- Tính số học sinh loại khá trở lên ở cả 2 môn.
- Xác suất thực nghiệm=Số học sinh được loại khá trở lên ở cả 2 môn:Tổng số học sinh được lựa chọn.
Tổng số học sinh là tổng tất cả các số trên bảng: 170.
Các học sinh được loại khá trở lên ở cả 2 môn:
+ Toán giỏi, Ngữ văn giỏi: 40
+ Toán giỏi, Ngữ văn khá: 20
+ Toán khá, Ngữ văn giỏi: 15
+ Toán khá, Ngữ văn khá: 30
Số học sinh được loại khá trở lên ở cả 2 môn là:
40+20+15+30=105
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên được loại khá trở lên ở cả 2 môn là \(\dfrac{{105}}{{170}} = \dfrac{{21}}{{34}}\)
Loại trung bình ở ít nhất một môn
-
A.
\(\dfrac{{13}}{{17}}\)
-
B.
\(\dfrac{{13}}{{34}}\)
-
C.
\(\dfrac{{21}}{{34}}\)
-
D.
\(\dfrac{1}{2}\)
Đáp án: B
- Xét các trường hợp loại trung bình ở ít nhất một môn.
- Tính số học sinh được loại trung bình ở ít nhất một môn.
- Xác suất thực nghiệm=Số học sinh bị loại trung bình ở ít nhất 1 môn: Tổng số học sinh.
Tổng số học sinh là 170.
Các học sinh được loại trung bình ở ít nhất một môn là:
+ Toán trung bình, Văn giỏi: 5
+ Toán trung bình, Văn khá: 15
+ Toán trung bình, Văn trung bình: 20
+ Văn trung bình, Toán giỏi: 15
+ Văn trung bình, Toán khá: 10
Số học sinh được loại trung bình ở ít nhất một môn là:
5+15+20+15+10=65
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả được loại trung bình ít nhất một môn:
\(\dfrac{{65}}{{170}} = \dfrac{{13}}{{34}}\).