1. Khi thiết kế một cái thang gấp, để đảm bảo an toàn người thợ đã làm thêm một thanh ngang để giữ cố định ở chính giữa hai bên thang (như hình vẽ bên) sao cho hai chân thang rộng một khoảng là 80 cm. Hỏi người thợ đã làm thanh ngang đó dài bao nhiêu cm?

2. Cho tam giác ABC (AB \( \ne \) AC; BC \( \ne \) AC) có đường cao BH (H nằm giữa A và C). Gọi các điểm D, E, F lần lượt là trung điểm của các cạnh AB, AC và BC.
a) Tứ giác BDEF là hình gì? Vì sao?
b) Chứng minh hai điểm H và B đối xứng nhau qua DF.
c) Tìm điều kiện của tam giác ABC để tứ giác BDEF là hình chữ nhật.
1. Dựa vào tính chất của đường trung bình để tính.
2.
a) Chứng minh BDEF có hai cạnh đối song song và bằng nhau.
b) Gọi K là giao điểm của DF và BH. Chứng minh DF \( \bot \) BH tại K và BK = KH.
c) Để BDEF là hình chữ nhật thì cần thêm điều kiện có một góc vuông.
1.
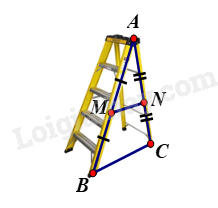
Gọi MN là thanh ngang; BC là độ rộng giữa hai bên thang.
MN nằm chính giữa thang nên M; N là trung điểm AB và AC.
Suy ra MN là đường trung bình của tam giác ABC.
Suy ra MN = \(\frac{1}{2}BC = \frac{1}{2}.80 = 40\,\,(cm)\).
Vậy người thợ đã làm thanh ngang đó dài 40 cm.
2.
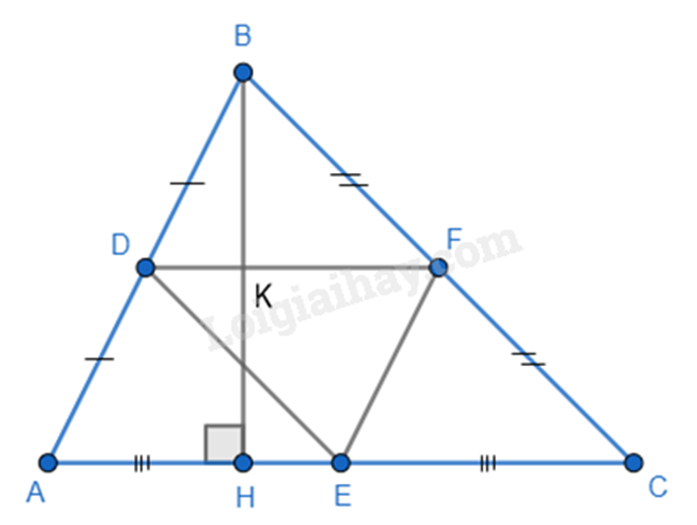
a) Ta có D, E là trung điểm của AB và AC nên DE là đường trung bình của tam giác ABC, khi đó DE // BC và DE = \(\frac{1}{2}\) (1)
Mà F là trung điểm của BC nên BF = FC = \(\frac{1}{2}\) BC. (2)
Từ (1) và (2) suy ra DE // BF (F \( \in \) BC) và DE = BF (=\(\frac{1}{2}\)BC) => BDEF là hình bình hành.
b) Tương tự, ta chứng minh được DF // AC; mà BH \( \bot \) AC nên BH \( \bot \) DF.
Gọi K là giao điểm của BH và DF.
Xét tam giác ABH có DK // AH; D là trung điểm của AB nên K là trung điểm của BH, hay BK = KH.
Do đó B và H đối xứng với nhau qua DF.
c) BDEF là hình chữ nhật khi và chỉ khi \(\widehat B = {90^0}\). Khi đó tam giác ABC vuông tại B.