Khu bảo tồn Muttart là một phần biểu tượng của cảnh quan

Đề bài

1. Khu bảo tồn Muttart là một phần biểu tượng của cảnh quan thành phố Edmonton, Canada với bốn nhà kính dạng kim tự tháp. Mỗi tòa nhà đều có từng chủ đề riêng. Hai nhà kính lớn đều có dạng hình chóp tứ giác đều với chiều cao 24m và diện tích đáy mỗi nhà kính khoảng $660{m^2}$. Tính tổng thể tích hai nhà kính này.

2. Cho $\Delta ABC$ nhọn (AB < AC). Hai đường cao BE và CF.

a) Chứng minh $\Delta ABE\backsim \Delta ACF$ và $AE.AC = AF.AB$

b) Trên tia BE lấy điểm N sao cho $\widehat {ANC} = {90^0}$ (E nằm giữa B và N). Chứng minh $\Delta ANE\backsim \Delta ACN$ và $A{N^2} = AE.AC$.

c) Trên cạnh CF lấy điểm M sao cho AM = AN. Tính số đo $\widehat {AMB}$.

Phương pháp giải

1. Tính thể tích của một nhà kính bằng công thức tính thể tích hình chóp tứ giác đều.

2. a) Chứng minh $\Delta ABE\backsim \Delta ACF$ theo trường hợp góc – góc suy ra tỉ số các cạnh tương ứng suy ra $AE.AC = AF.AB$.

b) Chứng minh $\Delta ANB\backsim \Delta ENA$ (g.g) suy ra tỉ số các cặp cạnh tương ứng bằng nhau suy ra $A{N^2} = NE.NB$.

c) Dựa vào các tỉ số của câu a và b suy ra $\frac{{AM}}{{AF}} = \frac{{AB}}{{AM}}$ suy ra $\Delta AMF\backsim \Delta ABM\left( c.g.c \right)$.

Từ đó suy ra số đo góc AMB.

Vì mỗi nhà kính lớn có dạng hình chóp tứ giác đều nên thể tích một nhà kính là:

$\frac{1}{3}.24.660 = 5280\left( {{m^3}} \right)$

Thể tích hai nhà kính này là:

$2.5280 = 10560\left( {{m^3}} \right)$

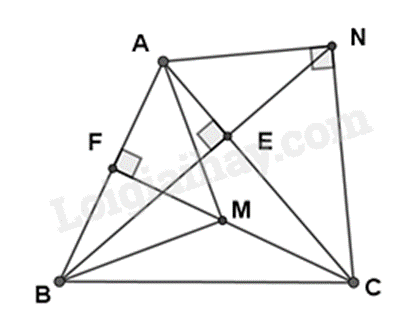
a) Xét $\Delta ABE$ và $\Delta ACF$ có:

$\widehat {AEB} = \widehat {AFC} = {90^0}$

$\widehat {BAC}$ chung

Suy ra $\Delta ABE\backsim \Delta ACF$ (g.g). (đpcm)

Suy ra $\frac{{AB}}{{AC}} = \frac{{AE}}{{AF}}$ hay $AB.AF = AE.AC$(đpcm) (1)

b) Xét $\Delta ANE$ và $\Delta ACN$ có:

$\widehat {AEN} = \widehat {ANC} = {90^0}$

$\widehat {NAC}$ chung

Suy ra $\Delta ANE\backsim \Delta ACN$ (g.g).

Suy ra $\frac{{AN}}{{AC}} = \frac{{AE}}{{AN}}$ hay $A{N^2} = AC.AE$ (đpcm). (2)

c) Từ (1) và (2) suy ra $AB.AF = A{N^2}$.

Mà AM = AN (gt) suy ra $AM = AB.AF$ hay $\frac{{AM}}{{AF}} = \frac{{AB}}{{AM}}$.

Xét $\Delta AMF$ và $\Delta ABM$ có:

$\widehat {BAM}$ chung

$\frac{{AM}}{{AF}} = \frac{{AB}}{{AM}}$ (cmt)

Suy ra $\Delta AMF\backsim \Delta ABM\left( c.g.c \right)$

Suy ra $\widehat {AMB} = \widehat {AFM} = {90^0}$.