Lý thuyết Các phép tính trong tập hợp số tự nhiên Toán 6 Chân trời sáng tạo
Tải vềLý thuyết Các phép tính trong tập hợp số tự nhiên Toán 6 Chân trời sáng tạo ngắn gọn, đầy đủ, dễ hiểu
1. Phép cộng và phép nhân
Phép cộng (+) và phép nhân \(\left( \times \right)\)các số tự nhiên đã được biết đến ở Tiểu học.
Chú ý: Trong một tích mà các thừa số đều bằng chữ hoặc chỉ có một thừa số bằng số ta có thể không viết dấu nhân ở giữa các thừa số; dấu “\( \times \)” trong tích các số cũng có thể thay bằng dấu “.”.
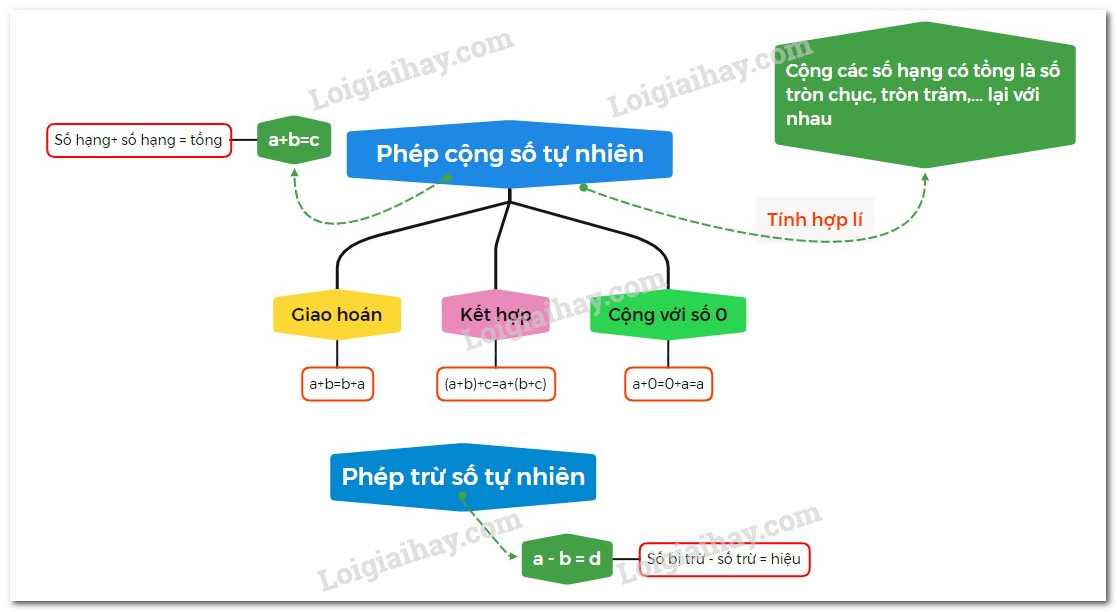
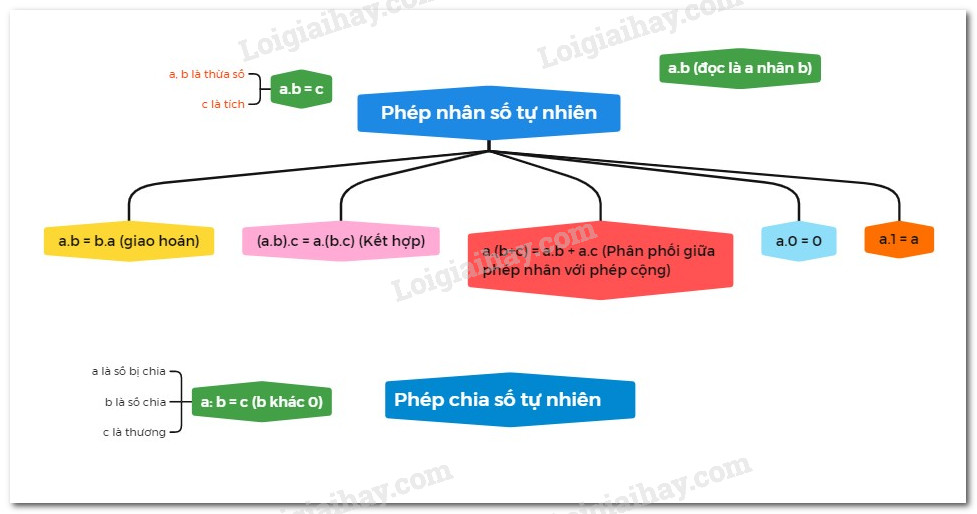
2. Tính chất của phép cộng và phép nhân số tự nhiên
Với a, b, c là các số tự nhiên, ta có:
- Tính chất giao hoán:
\(a + b = b + a\)
\(a.b = b.a\)
- Tính chất kết hợp:
\(\left( {a + b} \right) + c = a + \left( {b + c} \right)\)
\(\left( {a.b} \right).c = a.\left( {b.c} \right)\)
- Tính chất phân phối của phép nhân đối với phép cộng:
\(a.\left( {b + c} \right) = a.b + a.c\)
- Tính chất cộng với số 0, nhân với số 1:
\(a + 0 = a\)
\(a.1 = a\)
3. Phép trừ và phép chia hết
Ở Tiểu học ta đã biết cách tìn x trong phép toán b + x = a; trong đó a, b, x là các số tự nhiên, \(a \ge b\).Nếu có số tự nhiên x thỏa mãn b + x = a, ta có phép trừ a –b = x và gọc x là hiệu quả của phép trừ số a cho số b, a là số bị trừ, b là số trừ.
Tương tự với a, b là các số tự nhiên, \(b \ne 0\), nếu có số tự nhiên x thỏa mãn bx = a, ta có phép chia a : b = x và gọi a là số bị chia, b là số chia, x là thương của phép chia số a cho số b.
Chú ý : Phép nhân cũng có tính chất phân phối đối với phép trừ:
a.(b - c) = a.b – a.c