Lý thuyết diện tích hình thoi - Toán 4 — Không quảng cáo

Cho hình thoi $ABCD$ có $AC =m,\;BD=n$.

Cắt hình tam giác $AOD$ và hình tam giác $COD$ rồi ghép với hình tam giác $ABC$ để được hình chữ nhật $MNCA$ (xem hình vẽ).

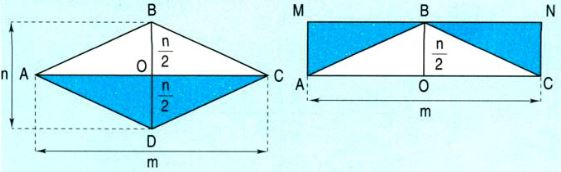
Dựa vào hình vẽ ta có:

Diện tích hình thoi $ABCD$ bằng diện tích hình chữ nhật $MNCA$.

Diện tích hình chữ nhật $MNCA$ là $m \times \dfrac{n}{2}$. Mà $m \times \dfrac{n}{2}=  \dfrac{m \times n}{2}$.

Vậy diện tích hình thoi $ABCD$ là $\dfrac{m \times n}{2}$.

Diện tích hình thoi bằng tích của độ dài hai đường chéo chia cho $2$ (cùng một đơn vị đo).

$S=\dfrac{m \times n}{2}$.

($S$ là diện tích của hình thoi; $m\,;\; n$ là độ dài của hai đường chéo).