Lý thuyết thực hành tính sai số trong phép đo. Ghi kết quả đo - Vật Lí 10
Phép đo trực tiếp và phép đo gián tiếp
BÀI 3. THỰC HÀNH TÍNH SAI SỐ TRONG PHÉP ĐO. GHI KẾT QUẢ ĐO
I. Phép đo trực tiếp và phép đo gián tiếp
- Phép đo trực tiếp là đo trực tiếp một đại lượng bằng dụng cụ đo, kết quả được đọc trực tiếp trên dụng cụ đo
- Phép đo gián tiếp là đo đại lượng không trực tiếp mà thông qua công thức liên hệ với các đại lượng có thể đo trực tiếp.
II. Sai số phép đo
1. Phân loại sai số
a) Sai số hệ thống
Nguyên nhân:
+ Chủ quan: do người đo
+ Khách quan: do dụng cụ
b) Sai số ngẫu nhiên
Cách khắc phục: tiến hành thí nghiệm nhiều lần và tính sai số.
2. Cách xác định sai số phép đo
- Sai số ngẫu nhiên tuyệt đối:
Bước 1: Tính giá trị trung bình: \(\overline A = \frac{{{A_1} + {A_2} + ... + {A_n}}}{n}\)
Bước 2: Tính sai số của từng lần đo:
\(\Delta {A_1} = \left| {\overline A - {A_1}} \right|;\Delta {A_2} = \left| {\overline A - {A_2}} \right|;...;\Delta {A_n} = \left| {\overline A - {A_n}} \right|\)
Bước 3: Tính sai số nguẫ nhiên tuyệt đối trung bình của n lần đo:
\(\overline {\Delta A} = \frac{{\Delta {A_1} + \Delta {A_2} + ... + \Delta {A_n}}}{n}\)
Bước 4: Sai số tuyệt đối của phép đo bằng tổng sai số ngẫu nhiên và sai số dụng cụ: \(\Delta A = \overline {\Delta A} + \Delta {A_{dc}}\)
3 . Cách xác định sai số phép đo gián tiếp
- Sai số tuyệt đối của một tổng hay hiệu bằng tổng các sai số tuyệt đối của các số hạng.
A = B + C
ΔA = ΔB + ΔC
- Sai số tỉ đối của một tích hay thương thì bằng tổng các sai số tỉ đối của các thừa số
A = B.C
\(\delta A = \delta B + \delta C\)
4 . Cách ghi kết quả đo
- Kết quả đo đại lượng A được ghi dưới dạng một khoảng giá trị:
\((\overline A - \Delta A) \le A \le (\overline A + \Delta A)\) hoặc \(A = \overline A \pm \Delta A\)
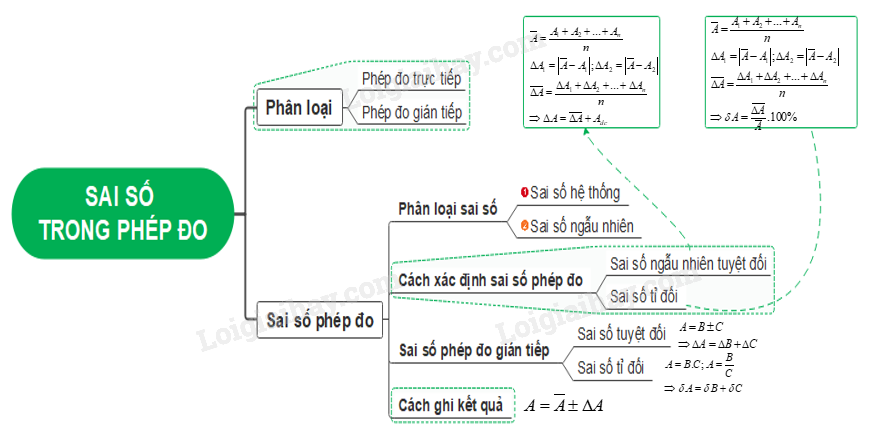
Sơ đồ tư duy về Sai số trong phép đo