Lý thuyết Từ thông. Hiện tượng cảm ứng điện từ - Vật lí 12 Kết nối tri thức
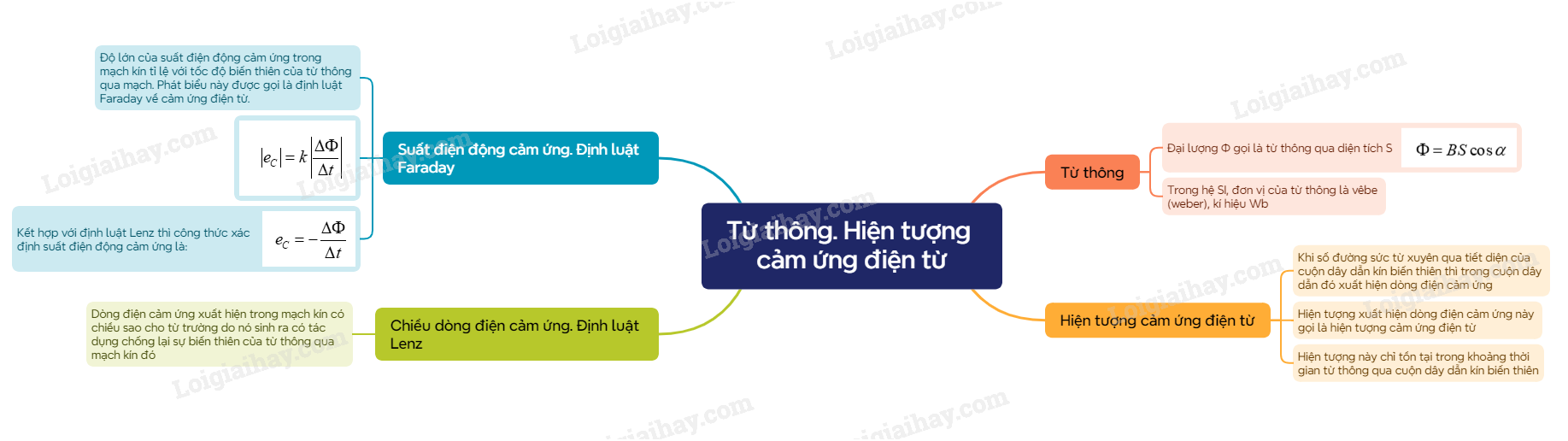
Từ thông Hiện tượng cảm ứng điện từ Chiều dòng điện cảm ứng. Định luật Lenz Suất điện động cảm ứng. Định luật Faraday
Bài 16. Từ thông. Hiện tượng cảm ứng điện từ
I. Từ thông

- Đại lượng \(\Phi \) gọi là từ thông qua diện tích S
\(\Phi = BS\cos \alpha \)
- Trong hệ SI, đơn vị của từ thông là vêbe (weber), kí hiệu Wb
\(1\;{\rm{Wb}} = 1\;{\rm{T}}{\rm{.}}{{\rm{m}}^2}\)
II. Hiện tượng cảm ứng điện từ
- Khi số đường sức từ xuyên qua tiết diện của cuộn dây dẫn kín biến thiên thì trong cuộn dây dẫn đó xuất hiện dòng điện cảm ứng và hiện tượng xuất hiện dòng điện cảm ứng này gọi là hiện tượng cảm ứng điện từ
- Hiện tượng này chỉ tồn tại trong khoảng thời gian từ thông qua cuộn dây dẫn kín biến thiên
III. Chiều dòng điện cảm ứng. Định luật Lenz
- Dòng điện cảm ứng xuất hiện trong mạch kín có chiều sao cho từ trường do nó sinh ra có tác dụng chống lại sự biến thiên của từ thông qua mạch kín đó – Định luật Lenz về chiều dòng điện cảm ứng
IV. Suất điện động cảm ứng. Định luật Faraday
- Thực nghiệm chứng tỏ rằng: Độ lớn của suất điện động cảm ứng trong mạch kín tỉ lệ với tốc độ biến thiên của từ thông qua mạch. Phát biểu này được gọi là định luật Faraday về cảm ứng điện từ.
- Nếu trong khoảng thời gian \(\Delta t\), từ thông qua mạch biến thiên một lượng \(\Delta \Phi \) thì \(\left| {\frac{{\Delta \Phi }}{{\Delta t}}} \right|\) là tốc độ biến thiên của từ thông. Vì vậy, ta có thể viết:
\(\left| {{e_C}} \right| = k\left| {\frac{{\Delta \Phi }}{{\Delta t}}} \right|\)
Trong hệ SI, hệ số tỉ lệ k = 1.
- Kết hợp với định luật Lenz thì công thức xác định suất điện động cảm ứng là:
\({e_C} = - \frac{{\Delta \Phi }}{{\Delta t}}\)
Dấu “-” biểu thị suất điện động cảm ứng ngược dấu với độ biến thiên từ thông.
Trong trường hợp mạch điện là một khung dây có N vòng dây thì: \({e_C} = - N\frac{{\Delta \Phi }}{{\Delta t}}\) với \(\Delta \Phi \) là độ biến thiên từ thông qua diện tích giới hạn bởi một vòng dây.
Sơ đồ tư duy về “Từ thông. Hiện tượng cảm ứng điện từ”