Lý thuyết viết các số đo khối lượng dưới dạng số thập phân

Ví dụ: Viết số thập phân thích hợp vào chỗ chấm:

1. Ôn tập bảng đơn vị đo khối lượng

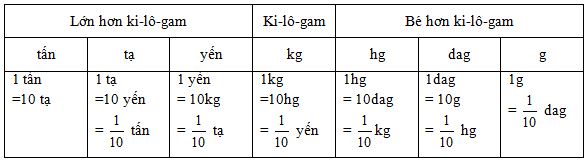
Nhận xét: Trong bảng đơn vị đo khối lượng, hai đơn vị đo liền nhau hơn (kém) nhau $10$lần, tức là:

- Đơn vị lớn gấp $10$ lần đơn vị bé;

- Đơn vị bé bằng $\dfrac{1}{{10}}$ đơn vị lớn.

2. Cách viết các số đo khối lượng dưới dạng số thập phân

Ví dụ 1: Viết số thập phân thích hợp vào chỗ chấm: $5$ tấn $246kg\, = \,...$ tấn.

Cách giải:

Theo bảng đơn vị đo khối lượng ta có $1$ tấn $ = 1000kg$ hay $1kg = \dfrac{1}{{1000}}$ tấn.

Nên $5$ tấn $246kg\,\, = \,\,5\dfrac{{246}}{{1000}}$ tấn $ = 5,246$ tấn

Vậy $5$ tấn $246kg\, = \,5,246kg$.

Ví dụ 2: Viết số thập phân thích hợp vào chỗ chấm: $12kg\,\,8g = ...kg$

Cách giải:

Theo bảng đơn vị đo khối lượng ta có $1kg = 1000g$ hay $1g = \dfrac{1}{{1000}}kg$.

Nên $12kg\,\,8g = 12\dfrac{8}{{1000}}kg = 12,008kg$

Vậy $12kg\,\,8g = 12,008kg$.

Ví dụ 3: Viết số thập phân thích hợp vào chỗ chấm: $135kg = ...$ tạ

Cách giải:

$135kg = 100kg + 35kg = 1$ tạ $35kg = 1\dfrac{{35}}{{100}}$ tạ $= 1,35$ tạ

Vậy $135kg = 1,35$ tạ.

Ví dụ 4: Viết số thích hợp vào chỗ chấm: $6,4kg = ...kg\,...dag$.

Cách giải:

$6,4kg = 6\dfrac{4}{{10}}kg = 6\dfrac{{40}}{{100}}kg = 6kg + \dfrac{{40}}{{100}}kg = 6kg\, + 40dag = 6kg\,40dag$.

Vậy $6,4kg = 6kg\,40dag$.

1. Ôn tập bảng đơn vị đo khối lượng

Nhận xét: Trong bảng đơn vị đo khối lượng, hai đơn vị đo liền nhau hơn (kém) nhau $10$lần, tức là:

- Đơn vị lớn gấp $10$ lần đơn vị bé;

- Đơn vị bé bằng $\dfrac{1}{{10}}$ đơn vị lớn.

2. Cách viết các số đo khối lượng dưới dạng số thập phân

Phương pháp chung:

- Xác định hai đơn vị đo khối lượng đã cho là gì và tìm được mối liên hệ giữa chúng.

- Viết số đo khối lượng đã cho thành phân số thập phân hoặc hỗn số có phần phân số là phân số thập phân.

- Viết phân số hoặc hỗn số vừa tìm được thành số thập phân gọn nhất.

Ví dụ 1: Viết số thập phân thích hợp vào chỗ chấm: $5$ tấn $246kg\, = \,...$ tấn.

Phương pháp:

- Xác định hai đơn vị đo khối lượng đã cho (tấn và $kg$) và tìm mối liên hệ giữa chúng: $1$ tấn $ = 1000kg$ hay $1kg = \dfrac{1}{{1000}}$ tấn.

- Đổi số đo khối lượng đã cho thành hỗn số có phần phân số là phân số thập phân.

- Đổi hỗn số vừa tìm được thành số thập phân gọn nhất.

Cách giải:

Theo bảng đơn vị đo khối lượng ta có $1$ tấn $ = 1000kg$ hay $1kg = \dfrac{1}{{1000}}$ tấn.

Nên $5$ tấn $246kg\,\, = \,\,5\dfrac{{246}}{{1000}}$ tấn $ = 5,246$ tấn

Vậy $5$ tấn $246kg\, = \,5,246kg$.

Ví dụ 2: Viết số thập phân thích hợp vào chỗ chấm: $12kg\,\,8g = ...kg$

Cách giải:

Theo bảng đơn vị đo khối lượng ta có $1kg = 1000g$ hay $1g = \dfrac{1}{{1000}}kg$.

Nên $12kg\,\,8g = 12\dfrac{8}{{1000}}kg = 12,008kg$

Vậy $12kg\,\,8g = 12,008kg$.

Ví dụ 3: Viết số thập phân thích hợp vào chỗ chấm: $135kg = ...$ tạ

Phương pháp:

- Xác định hai đơn vị đo khối lượng đã cho (tạ và $kg$) và tìm mối liên hệ giữa chúng: $1$ tạ $ = 100kg$ hay $1kg = \dfrac{1}{{100}}$ tạ.

- Đổi $135kg = 100kg + 35kg$, sau đó đổi $100kg$ sang đơn vị tạ rồi làm tiếp tương tự như những ví dụ bên trên.

Cách giải:

Cách 1: $135kg = 100kg + 35kg = 1$ tạ $35kg = 1\dfrac{{35}}{{100}}$ tạ $= 1,35$ tạ

Vậy $135kg = 1,35$ tạ.

Cách 2: Xác định các đơn vị nằm giữa tạ và ki-lô-gam: tạ, yến, kg.

Ta có bảng sau:

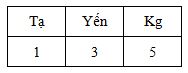
Đề bài yêu cầu đổi sang đơn vị là tạ nên ta đặt dấu phẩy sau số $1$.

Vậy $135kg = 1,35$ tạ.

Lưu ý: Ta có thể áp dụng cách 2 đối với bài viết các số đo độ dài hoặc số đo khối lượng dưới dạng số thập phân.

Cách giải nhanh: Khi đổi đơn vị đo khối lượng, ta dời dấu phẩy lần lượt sang phải (nếu đổi từ đơn vị lớn ra đơn vị nhỏ) hoặc sang bên trái (nếu đổi từ đơn vị nhỏ ra đơn vị lớn) một chữ số cho mỗi hàng đơn vị.

Ví dụ: $1,23kg = 12,3hg$ (đổi từ đơn vị lớn là $kg$ ra đơn vị nhỏ hơn là $hg$ và hai đơn vị này liền nhau trong bảng đơn vị nên ta dời dấu phẩy một hàng sang bên phải).

$12,3kg = 0,123$ tạ (đổi từ đơn vị bé là $kg$ sang đơn vị lớn hơn là tạ và trong bảng đơn vị ta có thứ tự $kg,$ yến, tạ nên ta dời dấu phẩy hai hàng sang bên trái).

Ví dụ 4: Viết số thích hợp vào chỗ chấm: $6,4kg = ...kg\,...dag$.

Phương pháp:

- Xác định hai đơn vị đo khối lượng đã cho ($kg$ và $dag$) và tìm mối liên hệ giữa chúng: $1kg = 100dag$ hay $1dag = \dfrac{1}{{100}}kg$ tạ.

- Viết $6,4kg$ dưới dạng hỗn số có phần phân số là phân số thập phân.

- Tách hỗn số thành phần nguyên và phần phân số, hai thành phần đều có đơn vị là $kg$

- Chuyển phần phân số với đơn vị là $kg$ sang đơn vị $dag$.

Cách giải:

$6,4kg = 6\dfrac{4}{{10}}kg = 6\dfrac{{40}}{{100}}kg = 6kg + \dfrac{{40}}{{100}}kg = 6kg\, + 40dag = 6kg\,40dag$.

Vậy $6,4kg = 6kg\,40dag$.