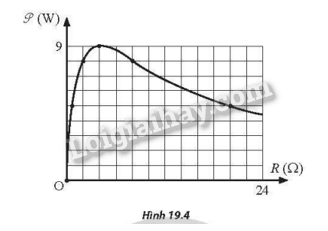
Mắc hai đầu một biến trở R vào hai cực của một nguồn điện không đổi. Điều chỉnh giá trị biến trở R. Bỏ qua điện trở của các dây nối. Đồ thị biểu diễn sự phụ thuộc của công suất toả nhiệt trên biến trở P theo R như Hình 19.4.
a) Công suất toả nhiệt trên biến trở: \({\rm{P}} = \frac{{{{\rm{E}}^2}}}{{R + 2r + \frac{{{r^2}}}{R}}}\)
b) Giá trị cực đại của P: \({{\rm{P}}_{{\rm{max}}}} = \frac{{{{\rm{E}}^2}}}{{4r}}\)
c) Suất điện động của nguồn điện là \({\rm{E}} = 12\;V\)
d) Khoảng thời gian giữa hai lần liên tiếp công suất Pđạt giá trị 5 W là \({\rm{\Delta }}t = 60{\rm{\;s}}\)
a) Công suất toả nhiệt trên biến trở: \({\rm{P}} = \frac{{{{\rm{E}}^2}}}{{R + 2r + \frac{{{r^2}}}{R}}}\)
b) Giá trị cực đại của P: \({{\rm{P}}_{{\rm{max}}}} = \frac{{{{\rm{E}}^2}}}{{4r}}\)
c) Suất điện động của nguồn điện là \({\rm{E}} = 12\;V\)
d) Khoảng thời gian giữa hai lần liên tiếp công suất Pđạt giá trị 5 W là \({\rm{\Delta }}t = 60{\rm{\;s}}\)
a) Ta có, công suất toả nhiệt trên biến trở: \({\rm{P}} = R{I^2} = R\frac{{{{\rm{E}}^2}}}{{{{\left( {R + r} \right)}^2}}} = \frac{{{{\rm{E}}^2}}}{{R + 2r + \frac{{{r^2}}}{R}}}\)
Đúng
b) Áp dụng bất đẳng thức Cauchy ta có: \(R + \frac{{{r^2}}}{R} \ge 2r\) Dấu "=" của biểu thức này ( R = r) tương ứng với giá trị cực đại của P: \({{\rm{P}}_{{\rm{max}}}} = \frac{{{{\rm{E}}^2}}}{{4r}}\)
Đúng
c) Từ đồ thị, ta có: r=4Ωvà P max =9 W.
Thay vào: \({{\rm{P}}_{\max }} = \frac{{{{\rm{E}}^2}}}{{4r}} \Rightarrow 9 = \frac{{{{\rm{E}}^2}}}{{4.4}} \Rightarrow {\rm{E}} = 12\;V\)
Đúng
d) Với P=5 W ta thấy trên đồ thị có một giá trị tương ứng là R 2 =20Ω. Giá trị R 1 còn lại thoả điều kiện R 1 R 2 =r 2 ⇒R 1 ⋅20=4 2 ⇒R 1 =0,8Ω
Từ đề bài, ta có: R=0,32t(Ω), (t tính bằng s). Từ đó, thời gian cần tìm là:
\({\rm{\Delta }}t = \frac{{20 - 0,8}}{{0,32}} = 60{\rm{\;s}}\)
Đúng