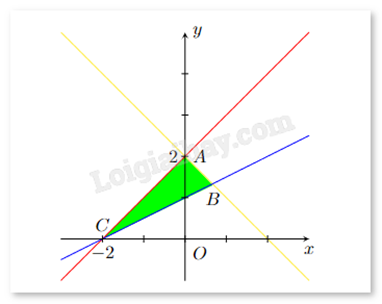
Miền tam giác (kể cả ba cạnh AB, BC, CA) trong hình vẽ sau biểu diễn miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình cho dưới đây?
-
A.
\(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \le 0}\\{x - y + 2 \ge 0}\\{x - 2y + 2 \le 0}\end{array}} \right.\)
-
B.
\(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \ge 0}\\{x - y + 2 \ge 0}\\{x - 2y + 2 \le 0}\end{array}} \right.\)
-
C.
\(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \le 0}\\{x - y + 2 \le 0}\\{x - 2y + 2 \le 0}\end{array}} \right.\)
-
D.
\(\left\{ {\begin{array}{*{20}{c}}{x + y - 2 \le 0}\\{x - y + 2 \ge 0}\\{x - 2y + 2 \ge 0}\end{array}} \right.\)
Thay tọa độ của điểm thuộc miền nghiệm vào các bất phương trình xem có thỏa mãn không.
Dùng phương pháp loại trừ.
Xét đáp án A:
Thay điểm có tọa độ \(\left( {0;\frac{3}{2}} \right)\) vào cả ba bất phương trình của hệ đều thỏa mãn.
Vậy đáp án A đúng.
Xét đáp án B:
Thay điểm có tọa độ \(\left( {0;\frac{3}{2}} \right)\) vào bất phương trình thứ nhất của hệ được \(0 + \frac{3}{2} - 2 \ge 0\) (vô lí).
Vậy bất phương trình ở đáp án B sai.
Xét đáp án C:
Thay điểm có tọa độ \(\left( {0;\frac{3}{2}} \right)\) vào bất phương trình thứ hai của hệ được \(0 - \frac{3}{2} + 2 \le 0\) (vô lí).
Vậy bất phương trình ở đáp án C sai.
Xét đáp án D:
Thay điểm có tọa độ \(\left( {0;\frac{3}{2}} \right)\) vào bất phương trình thứ ba của hệ được \(0 - 2.\frac{3}{2} + 2 \ge 0\) (vô lí).
Vậy bất phương trình ở đáp án D sai.
Đáp án : A