Một cái lều ở trại hè của học sinh có dạng hình chóp tứ

Đề bài

1. Một cái lều ở trại hè của học sinh có dạng hình chóp tứ giác đều với chiều cao của mặt bên xuất phát từ đỉnh của chiếc lều là 2,24m và cạnh đáy bằng 2m. Tính diện tích vải bạt cần thiết để dựng lều (không tính đến đường viền, nếp gấp), biết lều này không có đáy.

2. Cho tam giác ANE vuông tại A có đường cao AB.

a) Chứng minh $\Delta ANE\backsim \Delta BEA$ .

b) Chứng minh $A{N^2} = NB.NE$ .

c) Cho $AN = 15cm,NE = 25cm$ . Tia phân giác của góc N cắt cạnh AB tại I. Tính NI?

Phương pháp giải

1. Số bạt cần thiết để dựng lều chính là diện tích xung quanh của hình chóp tứ giác đều.

Sử dụng công thức tính diện tích xung quanh của chóp tứ giác đều.

2. a) Chứng minh $\Delta ANE\backsim \Delta BEA$ theo trường hợp góc – góc.

b) Chứng minh $\Delta ANB\backsim \Delta ENA$ (g.g) suy ra tỉ số các cặp cạnh tương ứng bằng nhau suy ra $A{N^2} = NE.NB$ .

c) Dựa vào $A{N^2} = NE.NB$ để tính NB.

Áp dụng định lí Pythagore vào $\Delta ANB$ để tính AB.

Áp dụng tính chất tia phân giác để tính BI suy ra BI.

Áp dụng định lí Pythagore vào tam giác $\Delta BIN$ để tính NI.

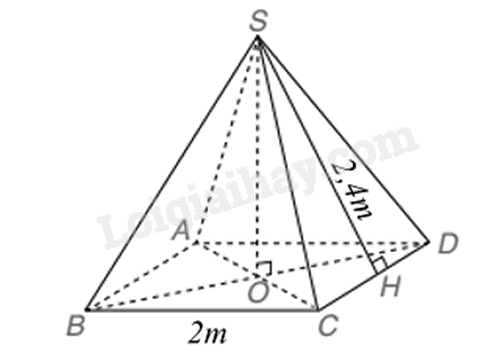
Gọi hình mô tả của cái lều là hình chóp S.ABCD (như hình vẽ).

Diện tích vải lều (diện tích xung quanh của chiếc lều) là:

${S_{xq}} = \frac{{4.2}}{2}.2,24 = 8,96\left( {{m^2}} \right)$

Vậy diện tích vải bạt cần thiết để dựng lều là $8,96{m^2}$ .

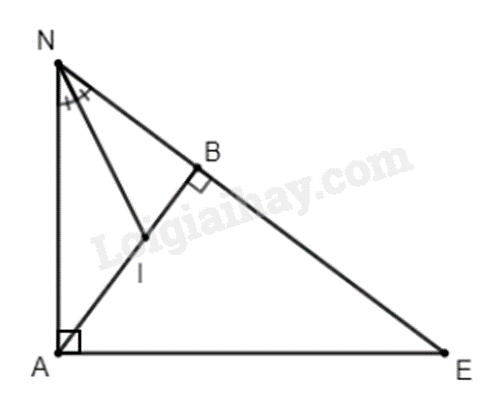
a) Xét $\Delta ANE$ và $\Delta BEA$ có:

$\widehat {NAE} = \widehat {EBA} = {90^0}$

$\widehat E$ chung

Suy ra $\Delta ANE\backsim \Delta BEA$ (g.g). (đpcm)

b) Xét $\Delta ANB$ và $\Delta ENA$ có:

$\widehat {ABN} = \widehat {EAN} = {90^0}$

$\widehat N$ chung

Suy ra $\Delta ANB\backsim \Delta ENA$ (g.g).

Suy ra $\frac{{AN}}{{NB}} = \frac{{NE}}{{AN}}$ hay $A{N^2} = NE.NB$ (đpcm).

c) Thay $AN = 15cm,NE = 25cm$ vào $A{N^2} = NE.NB$ (cmt), ta được:

${15^2} = 25.NB$ suy ra $NB = \frac{{{{15}^2}}}{{25}} = 9\left( {cm} \right)$

Áp dụng định lí Pythagore vào tam giác vuông ANB vuông tại B, ta có:

$A{B^2} = A{N^2} - N{B^2} = {15^2} - {9^2} = 144$ suy ra $AB = \sqrt {144} = 12\left( {cm} \right)$

NI là tia phân giác của góc ANB nên ta có:

$\frac{{AN}}{{NB}} = \frac{{AI}}{{IB}}$ hay $\frac{{AN}}{{AI}} = \frac{{BN}}{{BI}}$ .

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{{AN}}{{AI}} = \frac{{BN}}{{BI}} = \frac{{AN + BN}}{{AI + BI}} = \frac{{15 + 9}}{{AB}} = \frac{{24}}{{12}} = 2$

Suy ra $BI = \frac{{BN}}{2} = \frac{9}{2} = 4,5\left( {cm} \right)$

Áp dụng định lí Pythagore vào tam giác BIN ta có:

$NI = \sqrt {B{N^2} + B{I^2}} = \sqrt {{9^2} + 4,{5^2}} = \frac{{9\sqrt 5 }}{2}\left( {cm} \right)$

Vậy $NI = \frac{{9\sqrt 5 }}{2}cm$ .