Một chất điểm chuyển động theo quy luật st = 6t^2 - T^3

Đề bài

Con hãy điền từ / cụm từ/ số thích hợp vào các ô trống

Một chất điểm chuyển động theo quy luật $s(t) = 6{t^2} - {t^3}$ . Tính thời điểm t (giây) tại đó vận tốc v (m/s) của chuyển động tại giá trị lớn nhất.

Đáp án:

Đáp án

Đáp án:

Phương pháp giải

Lập bảng biến thiên và tìm giá trị lớn nhất của hàm số.

Theo giả thiết: $s(t) = 6{t^2} - {t^3}$ , $t \in (0; + \infty )$ .

Vận tốc của chuyển động là $v(t) = s'(t) = 12t - 3{t^2}$ .

Ta có: $v'(t) = 12 - 6t = 0 \Leftrightarrow t = 2$ .

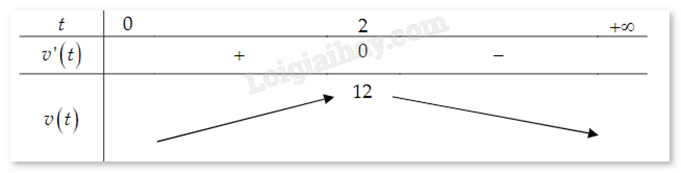
Dựa vào bảng biến thiên, ta thấy vận tốc đạt giá trị lớn nhất khi t = 2.