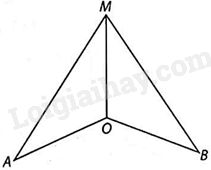
Một chiếc cột dựng trên nền sân phẳng. Gọi O là điểm đặt

Đề bài

Một chiếc cột dựng trên nền sân phẳng. Gọi O là điểm đặt chân cột trên mặt sân và M là điểm trên cột cách chân cột 30cm. Trên mặt sân, người ta lấy hai điểm A và B cách đều O là 40cm (A, B, O không thẳng hàng). Người ta đo độ dài MA và MB đều bằng 50cm.

Chọn khẳng định đúng.

A.
Tam giác MOB là tam giác tù.
B.
Tam giác MAO là tam giác nhọn.
C.
$MO \bot \left( {AOB} \right)$ .
D.
Cả A, B, C đều đúng.

Phương pháp giải

Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì $d \bot \left( P \right)$ .

Vì ${50^2} = {30^2} + {40^2}$ nên $M{A^2} = M{O^2} + O{A^2}$ và $M{B^2} = M{O^2} + O{B^2}$

Do đó, tam giác MOA vuông tại O và tam giác MOB vuông tại O.

Suy ra, $MO \bot OA,MO \bot OB$

Mà OA và OB cắt nhau tại O và nằm trong mặt phẳng (OAB). Do đó, $MO \bot \left( {AOB} \right)$ .

Đáp án C.

Đáp án : C