Một con lắc lò xo có độ cứng 50 N/m đang DĐĐH với đồ thị biểu diễn sự phụ thuộc của động năng và thế năng vào li độ như hình vẽ. Cơ năng của dao động bằng bao nhiêu J?
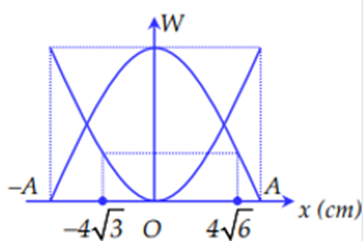
+ Đọc đồ thị W-x + Sử dụng biểu thức tính thế năng: \({W_t} = \frac{1}{2}k{x^2}\)
+ Sử dụng biểu thức tính cơ năng: \(W = {W_t} + {W_d}\)
Từ đồ thị ta có: + Tại vị trí: \({x_1} = 4\sqrt 6 cm\)
Thế năng của vật: \({W_{t1}} = \frac{1}{2}kx_1^2 = \frac{1}{2}.50.{(0,04\sqrt 6 )^2} = 0,24J\)
Động năng của vật: \({W_{d1}}\)
+ Tại vị trí: \({x_2} = - 4\sqrt 3 cm\)
Thế năng của vật: \({W_{t2}} = \frac{1}{2}kv_2^2 = \frac{1}{2}.50.{( - 0,04\sqrt 3 )^2} = 0,12J\)
Động năng của vật: \({W_{d2}}\) + Lại có: \({W_{{t_1}}} + {W_{{d_1}}} = {W_{{t_2}}} + {W_{{d_2}}} = W\)
Và từ đồ thị, ta có: \({W_{{d_1}}} = {W_{{t_2}}}\)
Ta suy ra:
\(\begin{array}{l}\left\{ \begin{array}{l}{W_{t1}} = 0,24J\\{W_{d1}} = 0,12J\end{array} \right.\\ \Rightarrow W = {W_{{t_1}}} + {W_{{d_1}}} = 0,24 + 0,12 = 0,36J\end{array}\)
Đáp án: 0,36