Đề bài
Con hãy điền từ / cụm từ/ số thích hợp vào các ô trống
Một cửa hàng bán một loại sản phẩm với lợi nhuận thu được khi bán x (trăm) sản phẩm được mô tả bởi hàm số \(L(x) = - 0,5{x^2} + 6x - 10\). Trong đó, x là số lượng sản phẩm bán ra, L(x) là lợi nhuận thu được (đơn vị: triệu đồng). Hãy xác định số lượng sản phẩm mà cửa hàng cần bán ra để lợi nhuận đạt mức cao nhất.
Đáp án:
Đáp án
Đáp án:
Phương pháp giải
Tìm x để hàm số \(L(x) = - 0,5{x^2} + 6x - 10\) đạt giá trị lớn nhất.
Lợi nhuận đạt mức cao nhất khi \(L(x) = - 0,5{x^2} + 6x - 10\) đạt giá trị lớn nhất.
Ta có: \(L'(x) = - x + 6 = 0 \Leftrightarrow x = 6\).
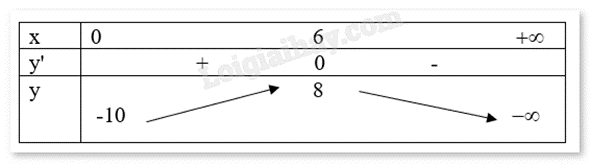
Theo bảng biến thiên, L(x) đạt giá trị lớn nhất khi x = 6 (trăm).
Vậy lợi nhuận đạt mức cao nhất khi bán ra 600 sản phẩm.