Một cuốn lịch để bàn có hình dạng là một hình chóp tam giác đều có các mặt là các tam giác đều có cạnh bằng 20cm. Tính thể tích của cuốn lịch. (làm tròn đến chữ số thập phân thứ hai).

Sử dụng tính chất của đường cao trong tam giác đều để tính AI.
Dựa vào tính chất của trọng tâm để tính OI.
Vì các mặt đều là tam giác đều nên đường cao của các tam giác bằng nhau, tính được SI.
Áp dụng định lí Pythagore trong tam giác để tính SO.
Sử dụng công thức tính thể tích hình chóp đều để tính thể tích của \(S.ABC\).
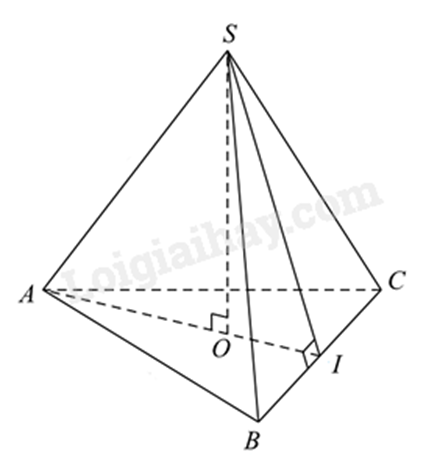
Xét \(\Delta ABC\) đều có đường cao \(AI = \frac{{AC\sqrt 3 }}{2} = \frac{{20\sqrt 3 }}{2} = 10\sqrt 3 \) (cm)
O là trọng tâm của tam giác ABC nên \(OI = \frac{1}{3}AI = \frac{1}{3}.10\sqrt 3 = \frac{{10\sqrt 3 }}{3}\)(cm).
Vì SI cũng là đường cao của tam giác đều SBC có cạnh bằng 20cm nên \(SI = AI = 10\sqrt 3 cm\).
Áp dụng định lí Pythagore vào tam giác vuông SOI, ta có:
\(\begin{array}{l}S{O^2} = S{I^2} - O{I^2} = {\left( {10\sqrt 3 } \right)^2} - {\left( {\frac{{10\sqrt 3 }}{3}} \right)^2} = \frac{{800}}{3}\\SO = \sqrt {\frac{{800}}{3}} = \frac{{20\sqrt 6 }}{3}\end{array}\)
Thể tích hình chóp S.ABC là: \(V = \frac{1}{3}.\frac{{20\sqrt 6 }}{3}.\frac{1}{2}.10\sqrt 3 .20 \approx 942,81\left( {c{m^3}} \right)\)
Vậy thể tích của cuốn lịch khoảng \(942,81c{m^3}\).