Một doanh nghiệp dự kiến lợi nhuận khi sản xuất x sản phẩm — Không quảng cáo

Một doanh nghiệp dự kiến lợi nhuận khi sản xuất x sản phẩm (\(0 \le x \le 300\)) được cho bởi hàm số \(y = - {x^3} + 300{x^2}\) (đơn

Đề bài

Một doanh nghiệp dự kiến lợi nhuận khi sản xuất x sản phẩm (\(0 \le x \le 300\)) được cho bởi hàm số \(y =  - {x^3} + 300{x^2}\) (đơn vị: đồng) và được minh họa bằng đồ thị ở hình bên dưới.

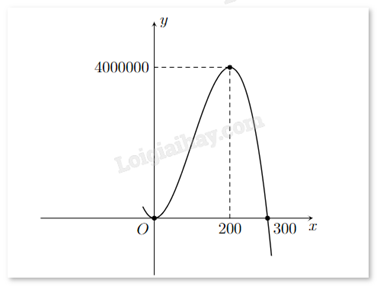
Doanh nghiệp cần sản xuất bao nhiêu sản phẩm để lợi nhuận dự kiến thu được nhiều nhất?

  • A.

    4000000

  • B.

    200

  • C.

    300

  • D.

    150

Phương pháp giải

Quan sát đồ thị và nhận xét.

Lợi nhuận đạt giá trị lớn nhất là 4000000 đồng khi sản xuất 200 sản phẩm.

Đáp án : B