Một electron bắt đầu bay vào điện trường đều E = 910V/m với vận tốc ban đầu v o = 3,2.10 6 m/s cùng chiều đường sức của E. Biết e = -1,6.10 -19 C; m = 9,1.10 −31 Kg. Cho rằng điện trường đủ rộng. Mô tả chuyển động tiếp theo của electron sau khi nó dừng lại.
a) Electron chuyển với gia tốc a = -1,6.10 14 m/s 2
b) Quãng đường electron đi được đến khi dừng lại là 32.10 -3
c) Sau khi dừng lại, electron chuyển chậm dần dần về vị trí lúc đầu xuất phát
d) Nếu điện trường chỉ tồn tại trong khoảng l = 3cm dọc theo đường đi của electron sẽ chuyển động đều với vận tốc 8.10 5 m/s sau khi ra khỏi điện trường.
a) Electron chuyển với gia tốc a = -1,6.10 14 m/s 2
b) Quãng đường electron đi được đến khi dừng lại là 32.10 -3
c) Sau khi dừng lại, electron chuyển chậm dần dần về vị trí lúc đầu xuất phát
d) Nếu điện trường chỉ tồn tại trong khoảng l = 3cm dọc theo đường đi của electron sẽ chuyển động đều với vận tốc 8.10 5 m/s sau khi ra khỏi điện trường.
Vận dụng công thức chuyển động của hạt trong điện trường
a)
Chọn trục Ox, có gốc O là vị trí mà electron bắt đầu bay vào điện trường, chiều dương trùng với chiều chuyển động
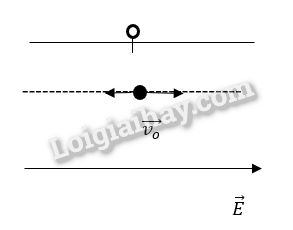
+ Khi bay trong điện trường, electron chịu tác dụng của lực điện \(\overrightarrow F \)
+ Theo định luật II Newton:\(\overrightarrow F = m.\overrightarrow a \) (1)
+ Vì q=e<0 nên \(\overrightarrow F \uparrow \downarrow \overrightarrow E \) mà \(\overrightarrow {{v_0}} \) cùng hướng với \(\overrightarrow E \) nên \(\overrightarrow F \) ngược chiều dương
Chiếu (1) lên Ox ta được: -F = ma ó|q|E = m.a
\(a = \frac{{ - \left| q \right|E}}{m} = \frac{{ - \left| {1,{{6.10}^{ - 19}}} \right|.910}}{{9,{{1.10}^{ - 31}}}} = - 1,{6.10^{14}}m/{s^2}\)
Vậy electron chuyển động chậm dần với gia tốc a = -1,6.10 14 m/
b) Thời gian chuyển động là:
\(\begin{array}{l}v = {v_0} + at \Rightarrow 0 = {v_0} + at\\ \Rightarrow t = \frac{{ - {v_0}}}{{at}} = \frac{{3,{{2.10}^6}}}{{1,{{6.10}^{14}}}} = {2.10^{ - 8}}s\end{array}\)
Quãng đường đi được của electron là:
\(s = \frac{{{v^2} - v_0^2}}{{2a}} = \frac{{0 - {{(3,{{2.10}^6})}^2}}}{{2.( - 1,{{6.10}^{14}})}} = {32.10^{ - 3}}m\)
c)
Sau khi dừng lại, electron vẫn chịu tác động của lực điện trường (ngược chiều dương) nên electron sẽ chuyển động nhanh dần đều về vị trí xuất phát. Và sau đó chuyển động thẳng đều với vận tốc đầu.
d)
Ta có: \(\begin{array}{l}{v^2} - v_0^2 = 2al\\ \Rightarrow v = \sqrt {2al + v_0^2} = \sqrt {2.( - 1,{{6.10}^{14}}){{.3.10}^{ - 2}} + {{(3,{{2.10}^6})}^2}} = {8.10^5}m/s\end{array}\)
Vậy khi ra khỏi điện trường, electron chuyển động thẳng đều với vận tốc 8.10 5 m/s
Đáp án
a) Đúng
b) Đúng
c) Sai
d) Đúng