Một hình lăng trụ đều tức là lăng trụ có đáy là đa giác đều — Không quảng cáo

Phương pháp giải

Để tìm được thể tích lăng trụ đứng khi đã biết chiều cao, ta cần tính diện tích đáy.

Thể tích = diện tích đáy . chiều cao

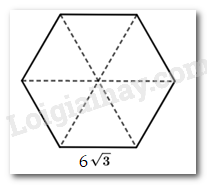
Gọi số cạnh của một đáy là \(n\). Khi đó số cạnh bên là \(n\).

Suy ra, tổng số cạnh của hình lăng trụ đứng là \(n + n + n = 3n\).

Theo đề bài, hình lăng trụ đều có tất cả 18 cạnh, ta có: \(3n = 18 \Rightarrow n = 6.\)

Vậy hình lăng trụ đứng đã cho là hình lăng trụ lục giác đều.

Có thể coi diện tích đáy là tổng diện tích của 6 tam giác đều, mỗi cạnh bằng \(6\sqrt 3 \) cm.

Do đó diện tích đáy là: \(S = \frac{{{{\left( {6\sqrt 3 } \right)}^2}.\sqrt 3 }}{4}.6 = 162\sqrt 3 \) ( cm ² )

Thể tích hình lăng trụ là:  \(V = S.h = 162\sqrt 3 .6\sqrt 3 \)= 2916 ( cm ³ )

Thể tích hình lăng trụ là 2916 ( cm ³ ).