Đề bài
Con hãy điền từ / cụm từ/ số thích hợp vào các ô trống
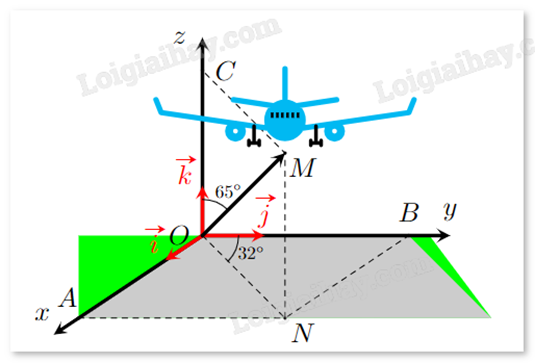
Một máy bay đang cất cánh từ phi trường. Với hệ tọa độ Oxyz được thiết lập như hình bên dưới, cho biết M là vị trí của máy bay, OM = 14, \(\widehat {NOB} = {32^o}\), \(\widehat {MOC} = {65^o}\). Khi đó, tọa độ điểm M có dạng (a;b;c), tính a + b + c (làm tròn đến hàng phần chục).
Đáp án:
Đáp án
Đáp án:
Phương pháp giải
Điểm M có hoành độ bằng OA, tung độ bằng OB và cao độ bằng OC.
Sử dụng hệ thức lượng trong tam giác để tính OA, OB, OC.
Ta có:
\(c = OC = OM.\cos {65^o} = 14.\cos {65^o}\).
\(b = OB = ON.\cos {32^o} = OM.\sin {65^o}.\cos {32^o} = 14.\sin {65^o}.\cos {32^o}\).
\(a = OA = ON.\cos ({90^o} - {32^o}) = OM\sin {65^o}.\cos {58^o} = 14.\sin {65^o}.\cos {58^o}\).
Vậy \(a + b + c \approx 23,4\).