Một nhà phân phối bánh gạo có hai nhà kho ở phía Đông và phía Tây của thành phố. Kho ở phía Đông có 80 thùng bánh gạo, kho ở phía Tây có 45 thùng bánh gạo. Sáng thứ Hai đầu tuần, đại lí A cần 50 thùng bánh gạo, đại lí B cần 70 thùng bánh gạo. Chi phí giao hàng cho mỗi thùng bánh gạo của kho ở phía Đông là 10 nghìn đồng cho đại lí A và 12 nghìn đồng cho đại lí B. Chi phí giao hàng cho mỗi thùng bánh gạo của kho ở phía Tây là 9 nghìn đồng cho đại lí A và 11 nghìn đồng cho đại lí B. Hỏi để chi phí vận chuyển là nhỏ nhất, nhà phân phối cần vận chuyển bao nhiêu thùng bánh gạo từ kho phía Tây cho đại lí A?
Đáp án:
Đáp án:
Lập hệ bất phương trình.
Gọi x, y \((x \ge 0,y \ge 0)\) lần lượt là số thùng bánh gạo được nhà phân phối chuyển từ kho phía Đông tới hai đại lí A và B.
Khi đó, 50 – x, 70 – y lần lượt là số thùng bánh gạo được nhà phân phối chuyển từ kho phía Tây tới hai đại lí A và B.
Vì kho phía Đông có tổng 80 thùng bánh gạo nên số thùng được chuyển đi nhỏ hơn hoặc bẳng 80. Từ đó suy ra \(x + y \le 80\).
Vì kho phía tây có tổng 45 thùng bánh gạo nên số thùng được chuyển đi nhỏ hơn hoặc bẳng 45. Từ đó suy ra \(50 - x + 70 - y \le 45\).
Ta có hệ bất phương trình \(\left\{ \begin{array}{l}x + y \le 80\\50 - x + 70 - y \le 45\\0 \le x \le 50\\0 \le y \le 70\end{array} \right.\) hay \(\left\{ \begin{array}{l}x + y \le 80\\x + y \ge 75\\0 \le x \le 50\\0 \le y \le 70\end{array} \right.\)
Tổng chi phí giao hàng là \(F(x;y) = 10x + 12y + (50 - x).9 + (70 - y).11 = 1220 + x + y\).
Để tìm miền nghiệm của hệ trên, ta vẽ các đường thẳng x + y = 80, x + y = 75, x = 50, y = 70 và tìm giao điểm của chúng.
Miền nghiệm biểu diễn là miền tứ giác ABCD có A(5;70), B(10;70), C(50;30), D(50;25) là giao điểm của các đường thẳng trên.
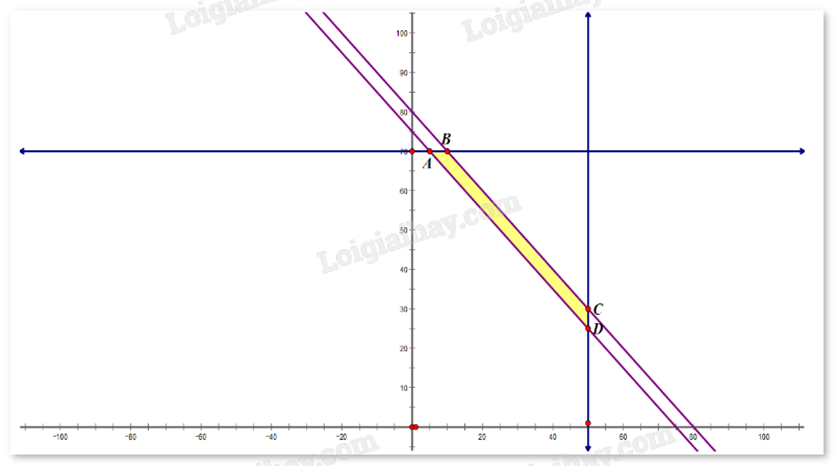
Tính giá trị của F(x;y) tại các đỉnh A, B, C, D tìm được giá trị nhỏ nhất là F(5;70) = 1220 + 5 + 70 = 1295.
Vậy nhà phân phối cần chuyển 5 thùng bánh gạo từ kho phía Đông và 45 thùng bánh gạo ở kho phía Tây cho đại lí A; 70 thùng bánh gạo từ kho phía Đông cho đại lí B.