Một ô tô có khối lượng là 4 tấn đang chuyển động đều trên — Không quảng cáo

Phương pháp giải

Áp dụng một số công thức:

+ Định luật 2 Newton: $\sum {\overrightarrow F }  = m.\overrightarrow a$

+ Công thức chuyển động biến đổi đều: $a = \frac{{{v^2} - v_0^2}}{{2.s}};v = {v_0} + at$

+ Công thức tính vận tốc trung bình: $\overline v  = \frac{s}{t}$

+ Công suất trung bình: $\overline P  = \overline v .t$

Đổi 54 km/h = 15 m/s; m = 4 tấn = 4000 kg.

Gia tốc chuyển động của ô tô là: $a = \frac{{{v^2} - v_0^2}}{{2s}} = \frac{{{{15}^2} - {{10}^2}}}{{2.250}} = 0,25(m/{s^2})$

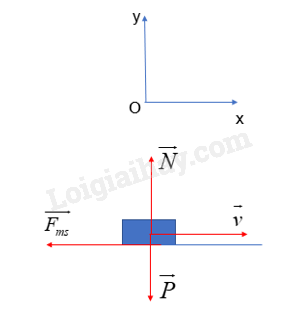
Khi ô tô chuyển động đều, ta có: $\overrightarrow P  + \overrightarrow N  + \overrightarrow {{F_k}}  + \overrightarrow {{F_{ms}}}  = m.\overrightarrow a  = \overrightarrow 0$     (*)

Chiếu (*) lên chiều dương của trục Ox, Oy, ta có:

$\begin{array}{l}\left\{ \begin{array}{l}N = P = m.g\\{F_k} - {F_{ms}} = 0\end{array} \right.\\ \Rightarrow {F_k} = {F_{ms}} = \mu .N = \mu mg\end{array}$

Mặt khác, ta có: ${P_{dc}} = {F_k}.v \Rightarrow {F_k} = \frac{{{P_{dc}}}}{v} = \frac{{20000}}{{10}} = 2000(N)$

Có: ${F_{ms}} = {F_k} \Leftrightarrow \mu mg = {F_k} \Rightarrow \mu  = \frac{{{F_k}}}{{mg}} = \frac{{2000}}{{4000.10}} = 0,05$

Khi vật tăng tốc đến v = 15 m/s

Theo định luật 2 Newton, ta có: $\overrightarrow P  + \overrightarrow N  + \overrightarrow {{F_k}}  + \overrightarrow {{F_{ms}}}  = m.\overrightarrow a$                          (**)

Chiếu (**) lên chiều dương của trục Oy, ta có: $N - P = 0 \Leftrightarrow N = P = mg$

Chiếu (**) lên chiều dương của trục Ox, ta có:

$\begin{array}{l}{F_k} - {F_{ms}} = m.a \Leftrightarrow {F_k} = {F_{ms}} + m.a\\ \Leftrightarrow {F_k} = \mu .N + m.a \Leftrightarrow {F_k} = \mu mg + ma\\ \Rightarrow {F_k} = 0,05.4000.10 + 4000.0,25 = 3000(N)\end{array}$

Thời gian ô tô tăng tốc là:

$t = \frac{{v - {v_0}}}{a} = \frac{{15 - 10}}{{0,25}} = 20(s)$

=> Vận tốc trung bình của ô tô trên quãng đường đó là:

$\overline v  = \frac{s}{t} = \frac{{250}}{{20}} = 12,5(m/s)$

=> Công suất trung bình của động cơ ô tô trên quãng đường đó là: $\overline P  = {F_k}.\overline v  = 3000.12,5 = 37500(W)$